Merge Sort is a sorting technique based on divide and conquer strategy. It is one of the efficient sorting algorithms as its worst case time complexity is of the order of nlog(n).
What is Merge Sort?
It is a sorting algorithm that makes use of Divide and Conquer method to sort an array of unsorted elements. It recursively breaks down an array(or a bigger problem) into arrays of smaller length(smaller and much simpler sub-problems) until each array contains only one element. Thereafter, it starts comparing the elements of each array and combines them likewise. After a series of comparisons and combining, it results in a sorted array at the end.
An example
Suppose you have this really old novel that you like. It is in a really shabby condition and all the pages are coming out of it. Accidentally, you drop this book and all the pages come out of it. Now all you have left is a bunch of unordered pages of this novel. How would you arrange them back in order?(provided that you can't buy this novel again if that's what you're thinking😂)
You can reorder them using Merge Sort algorithm! You can first divide the bundle of all the unorder pages into smaller bundles. Keep dividing them until you get groups of only single page, and then combine them one by one until you get all the pages sorted.
Algorithm
First we'll breakdown the array into sub arrays and then merge the sub arrays to get the final sorted array. The steps you can follow are as follows:
- let the array to be sorted be arr, of length n.
- set l = 0, this is the lower limit or the starting index of the array.
- set h = n-1, this is the upper limit or the end index of the array.
- set mid = (l+h)/2
- repeat the steps from 2-4 through recursion.
- one recursion for the left subarray from indices l to mid.
- one recursion for the right subarray from indices mid+1 to h.
- this will continue until l becomes equal to h (l!=h) or when each subarray contains single element.
- Then merge all the one elemented arrays after comparing them. Now, lets look at how the merging of the arrays can be done.
Algorithm for merging
This is the algorithm for the merging process. In the code, this algorithm will be used separately in a function called "merge".
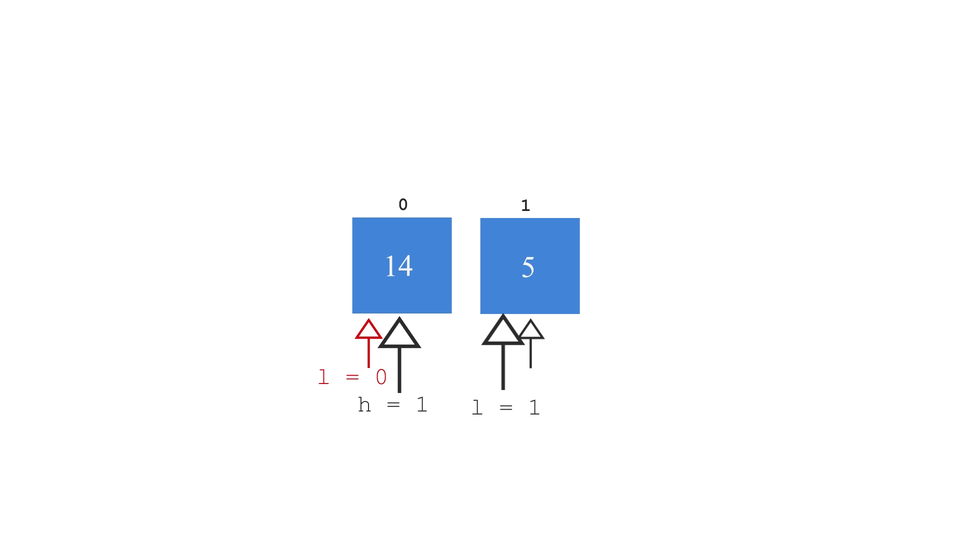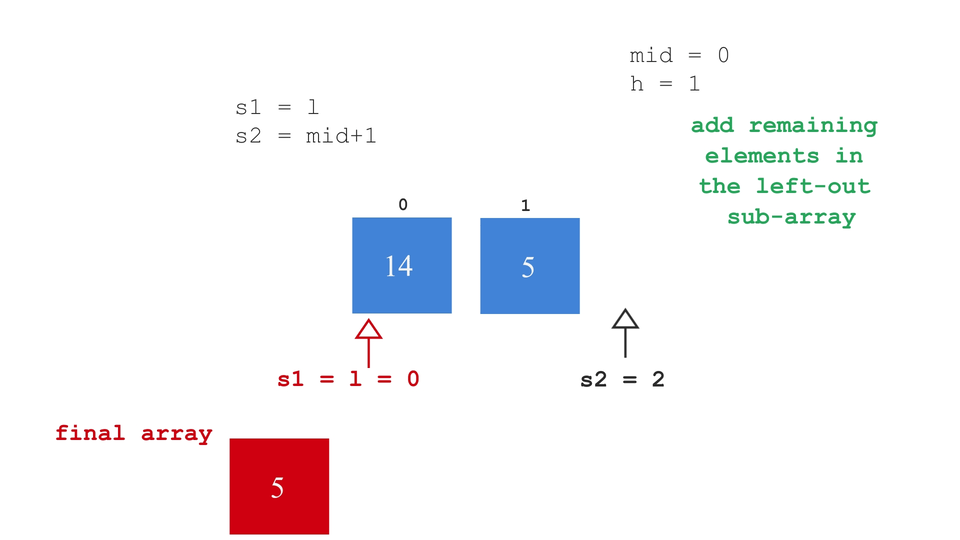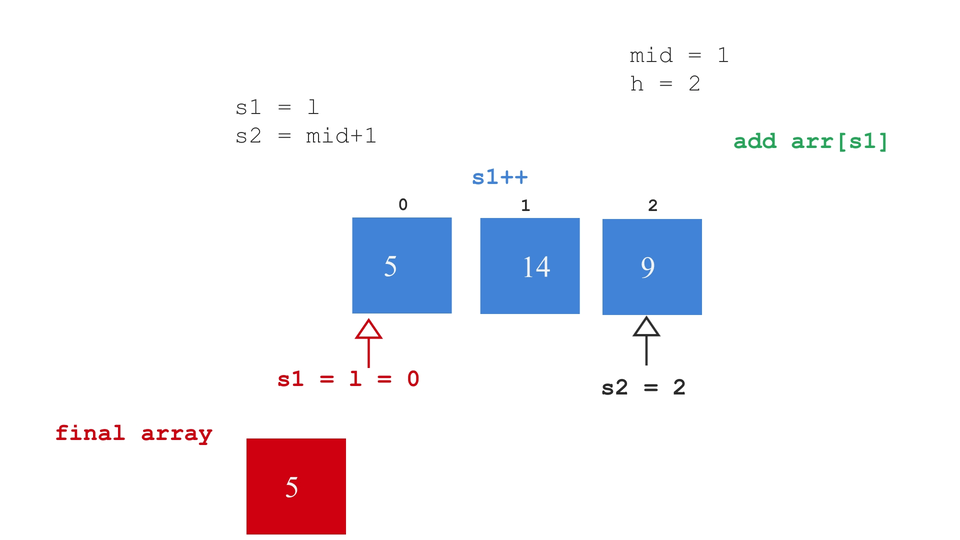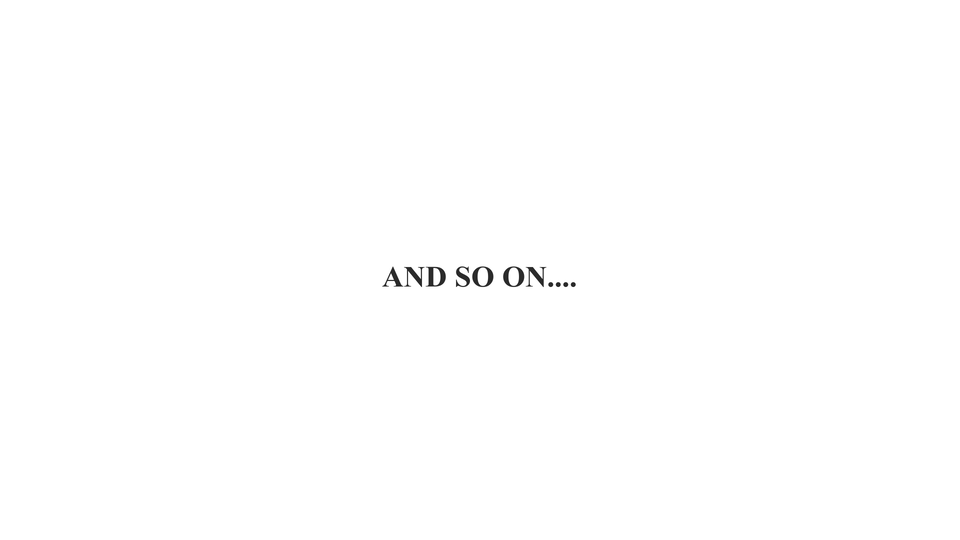
- set s1 = l, this is start index of the left sub-array.
- set s2 = mid+1, this is start index of the right sub-array.
- now iterate over the left sub-array by iterating over elements of arr from l to mid and iterate over the right sub-array by iterating over elements of arr from mid+1 to h.
- iterate until either of the two above conditions satisfy. We use "&" condition for that.
- while iterating, check which element is greater between arr[s1] and arr[s2]. Insert that element inside the final_array. This array is initially empty.
- By the end of this while loop, if either of the sub-array was incompletely iterated, then append the remaining elements of that sub-array into the final_array.
- Finally, insert the elements back in arr.
Every time the merge function will be called, the above process will be done and the final_arr will be copied into arr.
The division process of the algorithm might look something like this -
and the merge process looks something like this -
Code
Function for Merge Sort:
void mergeSort(int l, int h){
//find the mid element
if(l!=h){ //until both the start and end elements are the same
int mid = (l+h)/2;
//dividing into two separate arrays
mergeSort(l, mid); //for the left half
mergeSort( mid+1, h); //for the right half
//merge them
merge(l , mid, h);
}
}
Function for Merge:
void merge(int l, int mid, int h){
//make two arrays
int final_arr[SIZE];
int idx = 0;
int s1 = l;
int s2 = mid+1;
while(s1<=mid && s2<=h){
//iterate over the elements in both the arrays
if(arr[s1] > arr[s2]){
final_arr[idx] = arr[s2];
s2++;
}else{
final_arr[idx] = arr[s1];
s1++;
}
idx++;
}
//now append the rest of the elements from array 1 and 2
while(s1<=mid){
final_arr[idx]=arr[s1];
s1++;
idx++;
}
while(s2<=h){
final_arr[idx] = arr[s2];
s2++;
idx++;
}
//finally, transfer the elements to the sortedArray;
int i=l, j=0;
while(i<=h){
arr[i] = final_arr[j];
i++;
j++;
}
}
The full code:
#include <stdio.h>
#define SIZE 50
int arr[SIZE];
void merge(int l, int mid, int h){
//make two arrays
int final_arr[SIZE];
int idx = 0;
int s1 = l;
int s2 = mid+1;
while(s1<=mid && s2<=h){
//iterate over the elements in both the arrays
if(arr[s1] > arr[s2]){
final_arr[idx] = arr[s2];
s2++;
}else{
final_arr[idx] = arr[s1];
s1++;
}
idx++;
}
//now append the rest of the elements from array 1 and 2
while(s1<=mid){
final_arr[idx]=arr[s1];
s1++;
idx++;
}
while(s2<=h){
final_arr[idx] = arr[s2];
s2++;
idx++;
}
//finally, transfer the elements to the sortedArray;
int i=l, j=0;
while(i<=h){
arr[i] = final_arr[j];
i++;
j++;
}
}
void mergeSort(int l, int h){
//find the mid element
if(l!=h){ //until both the start and end elements are the same
int mid = (l+h)/2;
//dividing into two separate arrays
mergeSort(l, mid); //for the left half
mergeSort( mid+1, h); //for the right half
//merge them
merge(l , mid, h);
}
}
int main(){
int n;
printf("enter number of elements: ");
scanf(" %d", &n);
//get the array elements:
for(int i=0; i<n; i++){
printf("enter element: ");
scanf(" %d", &arr[i]);
}
int l=0; //the start element index
int h=n-1; //the end element index
//apply mergesort
mergeSort(l, h);
//finally, print the sorted array!
printf("SORTED ARRAY: ");
for(int i=0; i<n; i++){
printf("%d ", arr[i]);
}printf("\n");
}
Complexity
It much faster than the other sorting algorithm as we break the problem down and convert it into less complex problem. The array size reduces to half each time. As we use recursions in these problems, the time complexity can be computed by Master's theorem. Let's calculate the complexity of each step in it.
- division of the array - takes log(n) time as we know, whenever we divide the array into half, complexity is of log(n) order. We can also observed that in binary search.
- The merging process comprises of iterating over all the array elements. So, it takes time of order of n. Therefore, the worst case time complexity or big O notation for this algorithm is: O(n*log(n)).
Conclusion
The logic involved in Merge Sort algorithm is a little complicated to understand mostly because of the recursion part. In this article, I've tried to break it down and present it as simply as possible. Hope you liked reading this article. You can find more such articles here.
Thanks for reading!✨