A Max Heap is a Complete Binary Tree containing the largest value in the root node followed by smaller and smaller values in each succeeding layer. The last layer contains the smallest set of values of all the values. It looks something like this - 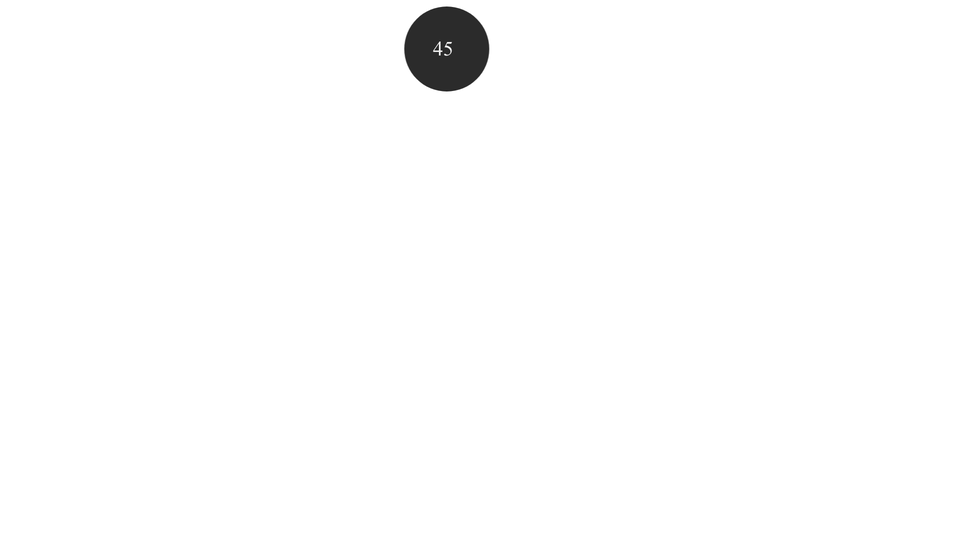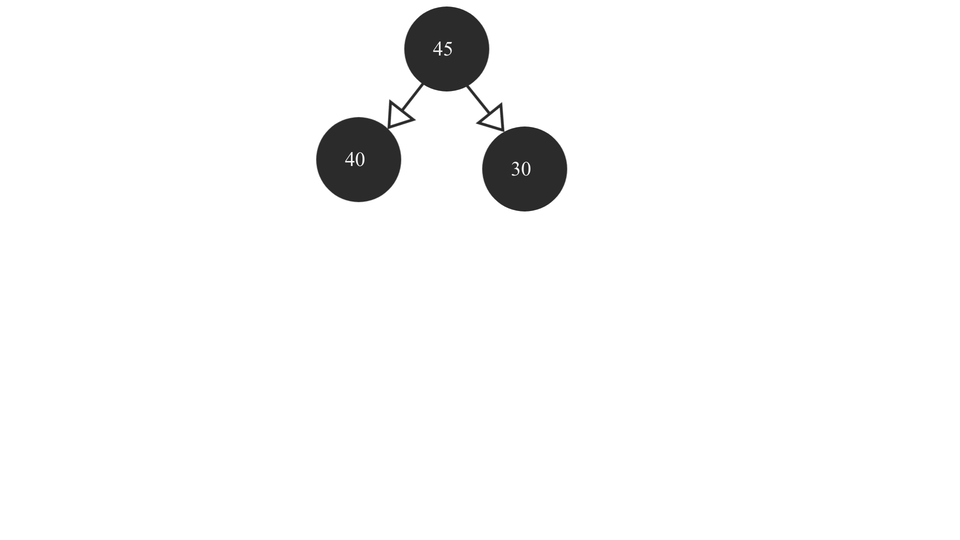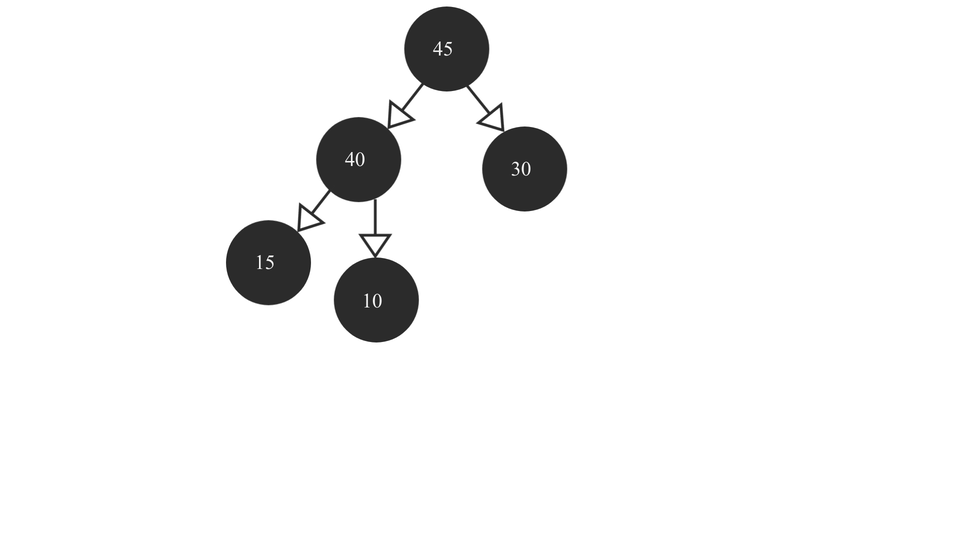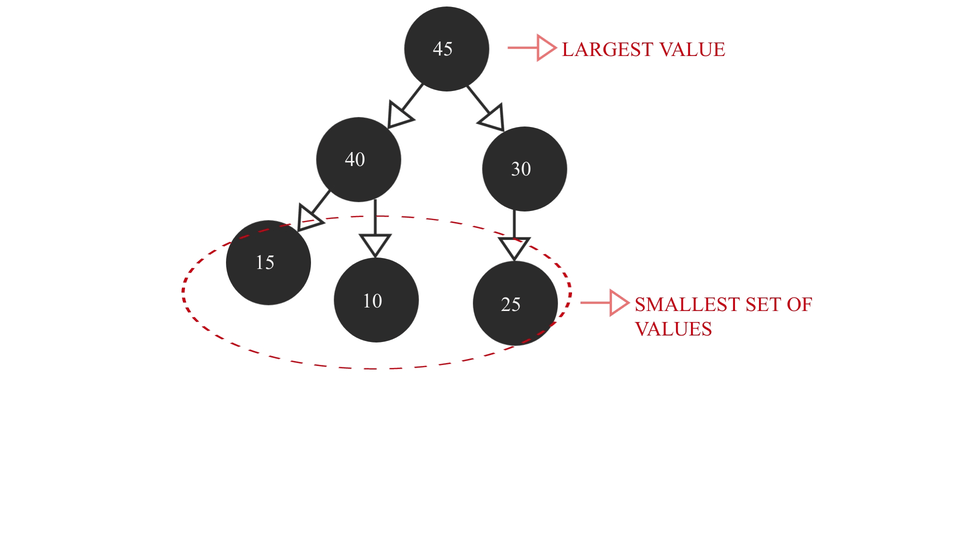
Now that we've got a slight idea about what a max Heap is, let's get started with its algorithm.
The Algorithm
Just like how we did in the Min Heap algorithm, we'll have to iterate to the right most parent node of the binary tree and from there we'll start the process of comparison and swap according to our condition.
Note that our condition here would be to see if the value of the child node is greater or less than the parent node's value. If it is greater, then we need to swap the value of the child and the parents. Otherwise, do nothing. As simple as that!
So, the algorithm is as follows:
- Find the right most parent node(let's call it "rmp") of the tree using the above function.
- Check if rmp has a right child node. In either case left child node would definitely be there as in either cases rmp is a "parent" node. So, compare rmp's data with its child node's data. If the child node's value is greater than rmp's value, swap their values, otherwise do nothing.
- Now, check if rmp's parent is NULL or not.
- If it is NULL, it means that rmp is actually pointing to the root node as no
other node in a tree can't have a parent node. To mark this visit to the root
node, we'll take a global variable(let's say count) initially equal to 0. Check
if the value of count is equal 0 or not.
- If it is equal to 0, it means that root node is being visited for the first time. In that case, increment the count by 1. Find the right most parent of rmp's(or root's) left subtree and then call heapify(this function) recursively with left subtree's rmp as its argument.
- If not equal to 0, it means that root node was already visited before, so just return the root node(or rmp) itself.
- If it is not NULL, then rmp is not the root node. So, first check if rmp is right
child or the left child of its parent node.
- If it is the right child, then call heapify(this function) on the left child of it's parent node so that comparison process can be done spread on to the left child.
- If it is the left child, then call heapify(this function) on the parent node itself for carrying out the comparison on the upper part of the tree.
- If it is NULL, it means that rmp is actually pointing to the root node as no
other node in a tree can't have a parent node. To mark this visit to the root
node, we'll take a global variable(let's say count) initially equal to 0. Check
if the value of count is equal 0 or not.
Additionally, I've made a separate algorithm for finding the right most parent or rmp. Following is the algorithm for it -
- Check if the root node is NULL or not.
- If it is - return root itself
- If not - do the following :
- check if the root node has a right child.
- if it does - recurse over the right subtree over and over until the rightmost parent node is found.
- If it doesn't - check if it has a left child node.
- If it does - it means, it is the right most parent node of the tree and so return the node itself.
- If it doesn't - return it's parent node as that would be the right most parent node in that case.
- check if the root node has a right child.
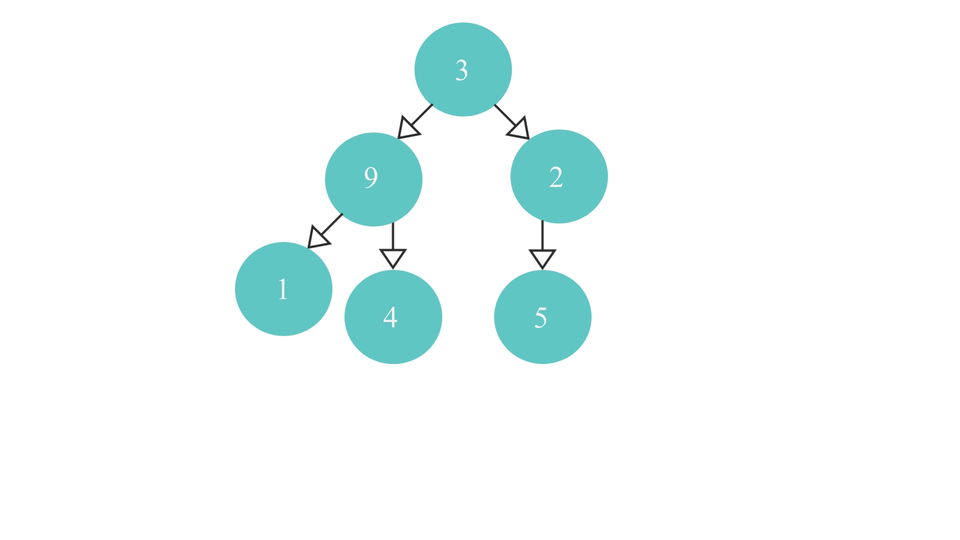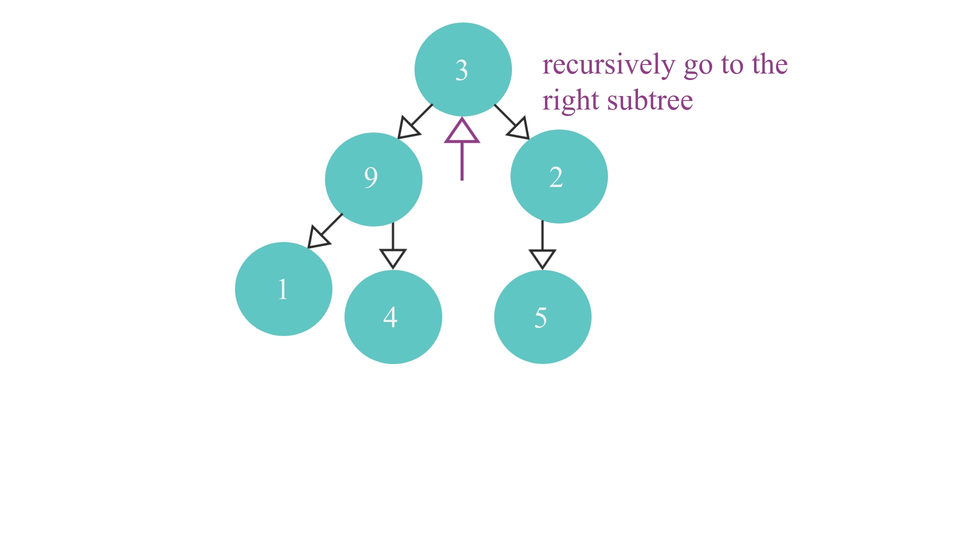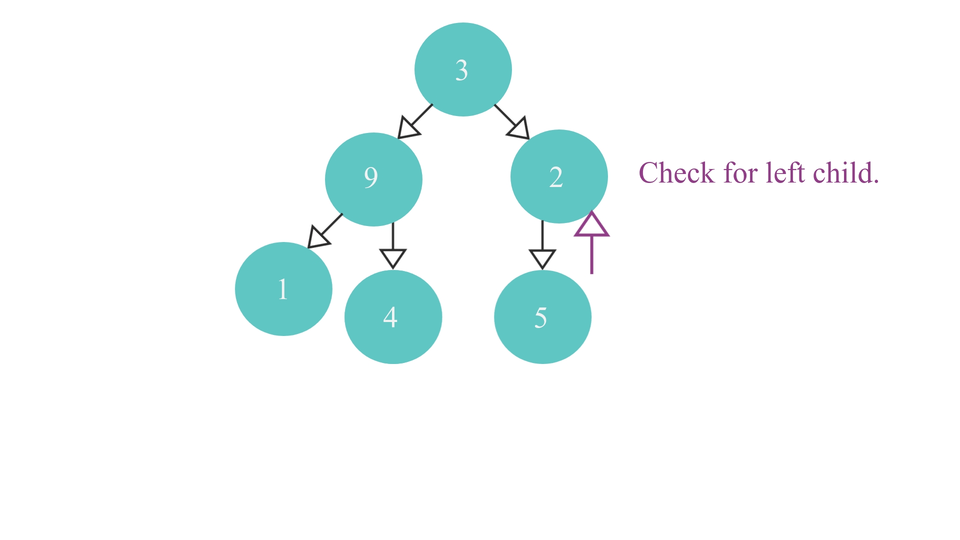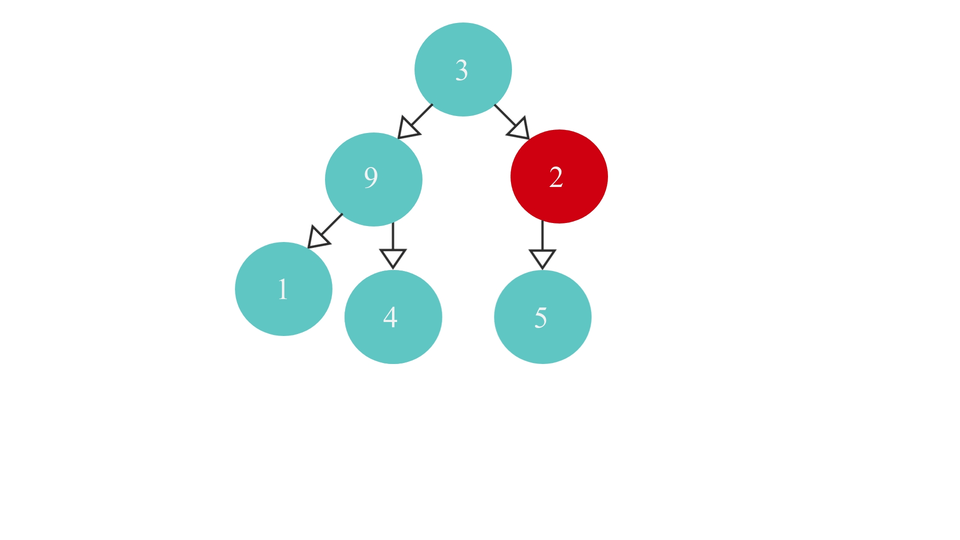
Finding the rmp node visually looks something like this -
The heapify process would look like this -
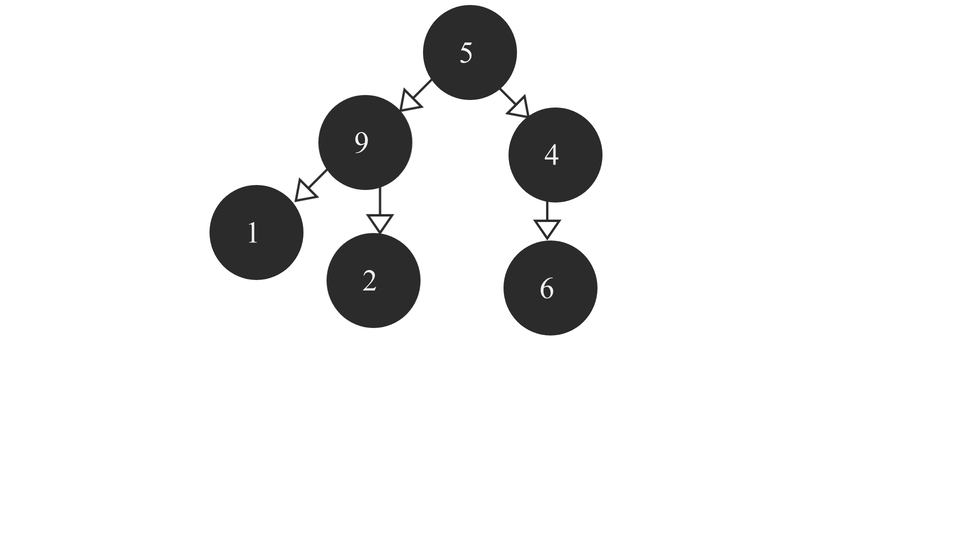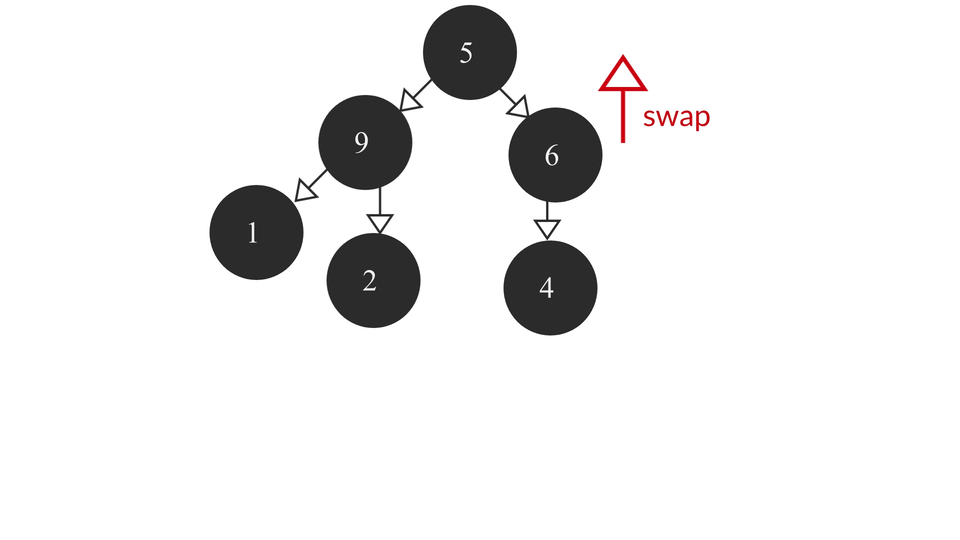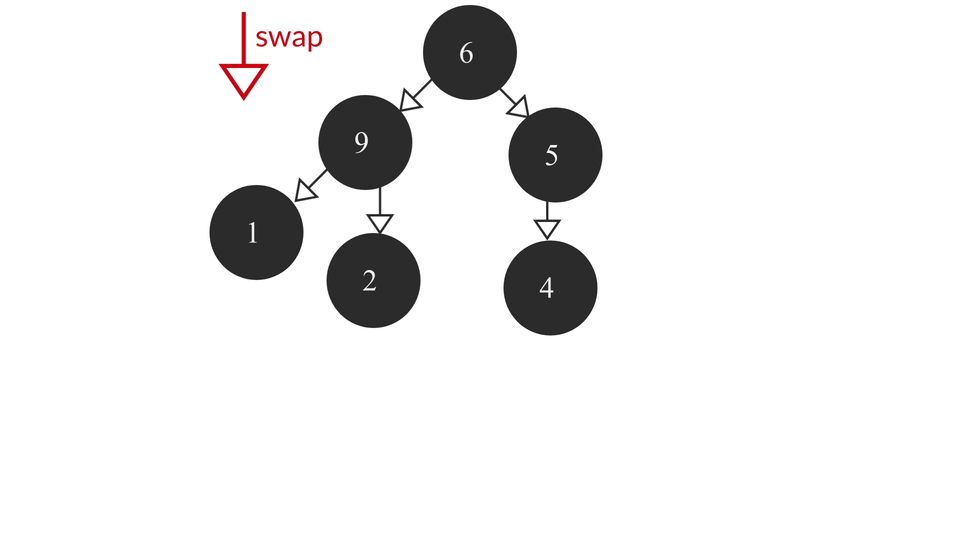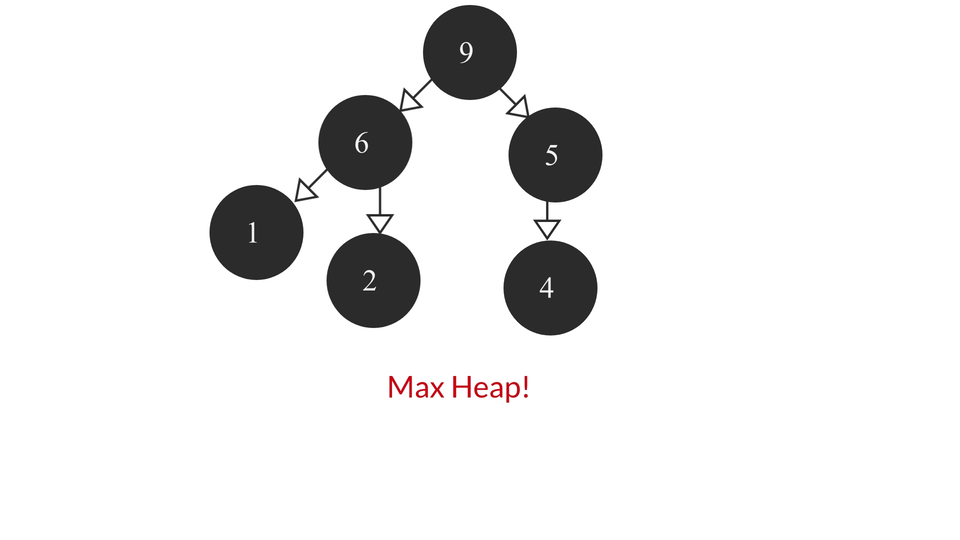
The code
In the code, I've made separate functions for finding the right most parent node and for carrying out the heapify process. The function for finding the right most parent is as follows -
NODE *reachRight(NODE *root){
if(root == NULL){
return root;
}else{
if(root->right==NULL){
//check if it has left child
if(root->left == NULL){
//node doesnt have a left AND a right child
//return Parent node
return root->parent;
}else{
//just return the current node as it is not a leaf node
//it has a left child
return root;
}
}else{
//it has both children
return reachRight(root->right);
}
}
}
The code for the heapify function is as follows:
void *heapify(NODE *rmp){
int temp;
//check for children of rmp;
if(rmp->right == NULL){
//it has only the left child.
//compare value with the left child
if(rmp->data < rmp->left->data){//check with the left child value
temp = rmp->data;
rmp->data = rmp->left->data;
rmp->left->data = temp;
}
}else{
//it has both the children
//compare values with both children
if(rmp->data < rmp->right->data){//check with the right child value
temp = rmp->data;
rmp->data = rmp->right->data;
rmp->right->data = temp;
}
if(rmp->data < rmp->left->data){//check with the left child value
temp = rmp->data;
rmp->data = rmp->left->data;
rmp->left->data = temp;
}
}
if(rmp->parent==NULL){ //rmp is the root node
if(count == 0){
//root node is being visited for the first time
NODE *rmpLeft = reachRight(rmp->left);
count++;
return heapify(rmpLeft);
}else{
//root node is being visited for the last time
return rmp;
}
}else{// if rmp is not root node
//first iterate over the left child of rmp's parent
if(rmp == rmp->parent->right){
return heapify(rmp->parent->left);
}else{
return heapify(rmp->parent);
}
}
}
Full code
#include <stdio.h>
#include <stdlib.h>
typedef struct node{
int data;
struct node *left;
struct node *right;
struct node *parent;
}NODE;
NODE *rootNode = NULL;
int count = 0;
NODE *createnode(int val){
NODE *newnode = (NODE *)malloc(sizeof(NODE));
newnode->data = val;
newnode->left = NULL;
newnode->right = NULL;
newnode->parent = NULL;
return newnode;
}
NODE *insertInTree(int val, NODE *root){
NODE *newnode = createnode(val);
if(root == NULL){
root = rootNode = newnode;
}else{
if(root->left == NULL){
root->left = newnode;
newnode->parent = root;
}else{
if(root->right == NULL){
root->right = newnode;
newnode->parent = root;
}else{
if(root->left->left==NULL || root->left->right==NULL){
return insertInTree(val, root->left);
}else if(root->right->left==NULL || root->right->right==NULL){
return insertInTree(val, root->right);
}else{
return insertInTree(val, root->left->left);
}
}
}
}
return root;
}
NODE *reachRight(NODE *root){
if(root == NULL){
return root;
}else{
if(root->right==NULL){
//check if it has left child
if(root->left == NULL){
//node doesnt have a left AND a right child
//return Parent node
return root->parent;
}else{
//just return the current node as it is not a leaf node
//it has a left child
return root;
}
}else{
//it has both children
return reachRight(root->right);
}
}
}
void inorder(NODE *root){
if(root == NULL){
return;
}else{
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
}
void *heapify(NODE *rmp){
int temp;
//check for children of rmp;
if(rmp->right == NULL){
//it has only the left child.
//compare value with the left child
if(rmp->data < rmp->left->data){//check with the left child value
temp = rmp->data;
rmp->data = rmp->left->data;
rmp->left->data = temp;
}
}else{
//it has both the children
//compare values with both children
if(rmp->data < rmp->right->data){//check with the right child value
temp = rmp->data;
rmp->data = rmp->right->data;
rmp->right->data = temp;
}
if(rmp->data < rmp->left->data){//check with the left child value
temp = rmp->data;
rmp->data = rmp->left->data;
rmp->left->data = temp;
}
}
if(rmp->parent==NULL){ //rmp is the root node
if(count == 0){
//root node is being visited for the first time
NODE *rmpLeft = reachRight(rmp->left);
count++;
return heapify(rmpLeft);
}else{
//root node is being visited for the last time
return rmp;
}
}else{// if rmp is not root node
//first iterate over the left child of rmp's parent
if(rmp == rmp->parent->right){
return heapify(rmp->parent->left);
}else{
return heapify(rmp->parent);
}
}
}
int main(){
//Insert
int arr[6] = {5,9,4,1,2,6};
for(int i=0; i<6; i++){
insertInTree(arr[i], rootNode);
}
printf("Inorder Traversal before: ");
inorder(rootNode);
printf("\n\n");
NODE *rmp = reachRight(rootNode);
heapify(rmp);
printf("\nInorder Traversal after: ");
inorder(rootNode);
}
As you can see, I've used a normal insertion function for the tree with some extra conditions so as to make it a complete binary tree.
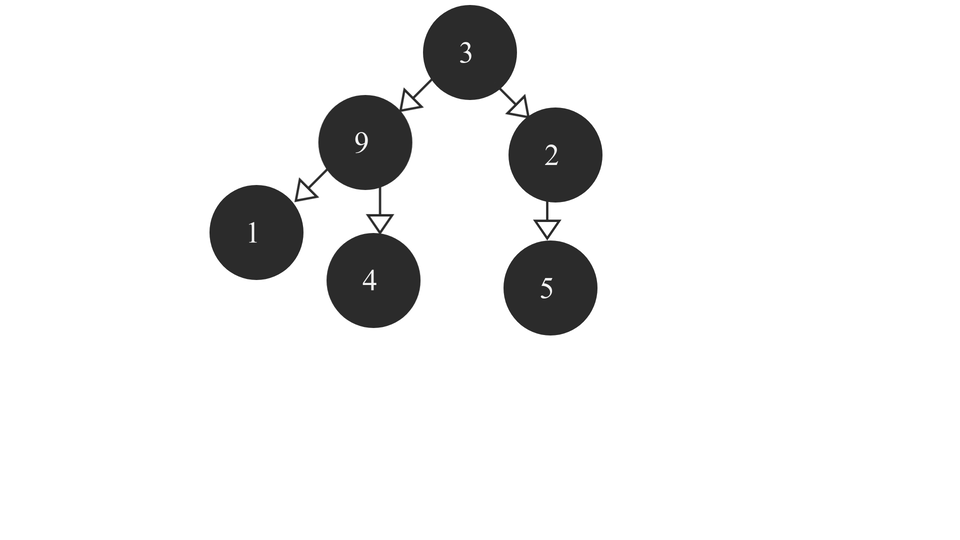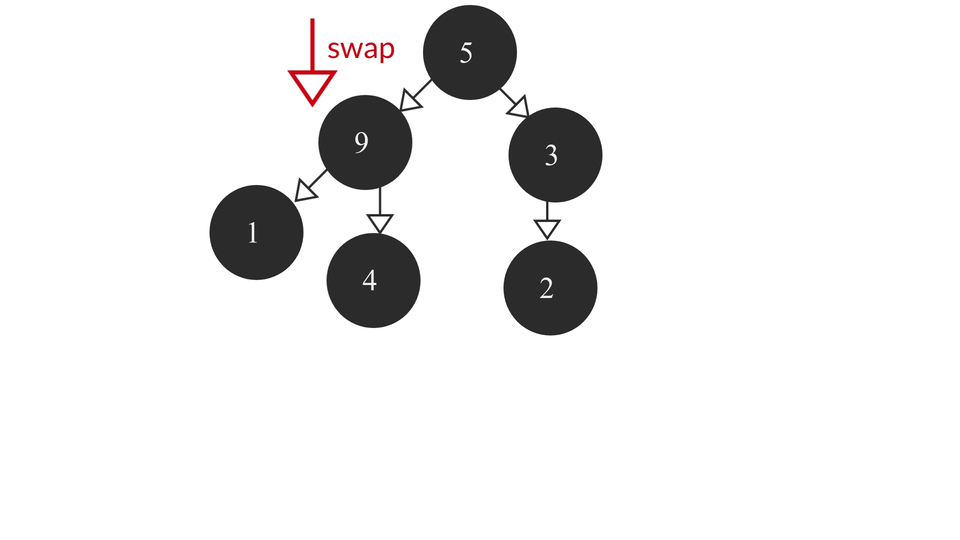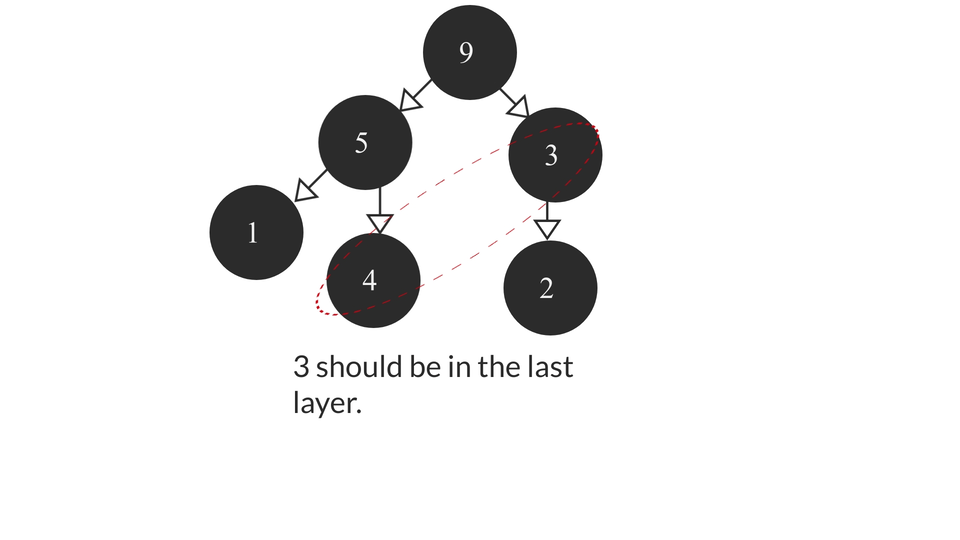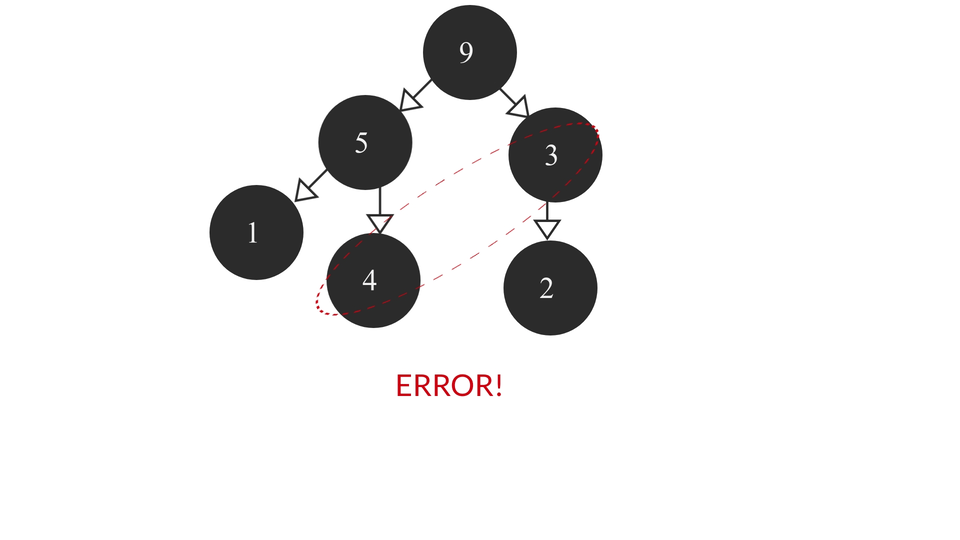
Problem with this approach
The above algorithm might fail at some conditions where comparisons cannot be done between two elements because they're in two different subtrees which may result in not all the smaller elements being able to make it to the last layer of tree. The above approach was used just for a better visualization of the whole process used in the algorithm. To achieve the right result in such a scenario would be a cumbersome process as we may have to compare the elements of each layer and the algorithm will become really complicated. That's why we don't usually implement heaps this way. Instead, we use arrays for the it.
Conclusion
I hope you liked reading this article. You can find more such articles on Data Structures and Algorithms here.
Happy Learning!🎄


