Linear Search and Binary Search are two popular searching algorithms. In this article, we'll be comparing the two algorithms in order to find out which algorithm is better based on their applications.
An Overview
Everyday we come across various situations wherein we find ourselves searching for things. Similarly, a computer always finds itself searching for data, files, folders, etc. in its memory whenever a user asks for it. But unlike our searching technique of haphazardly searching for an item for hours only to find it sitting on the couch, a computer always follows a logical way to go about it.
Searching algorithms are the kind of algorithms that a computer might make use of for searching. Linear Search and Binary Search are some very popular examples of search algorithms. These algorithms are mainly used for searching items in an array.
Which is better?
Now at this point, we need to find out the technique for searching that is best suited for our problem. Suppose we've been given an array of numbers and we need to find a number in it. Which approach do you think would be better? Binary search or Linear Search?
At first you might think Linear Search is a better option than Binary Search because it looks simpler. But that's not true.
In Linear search, each and every element is visited until the right element is found.
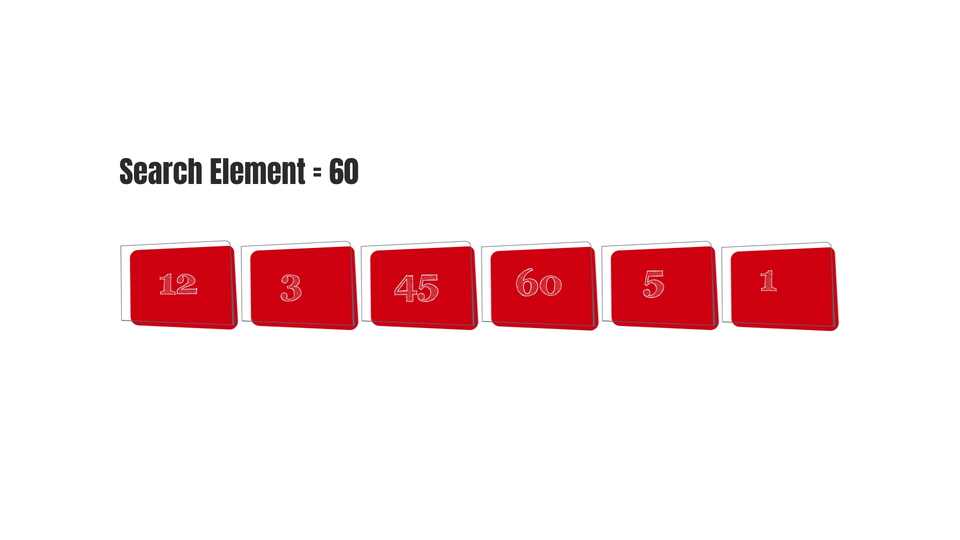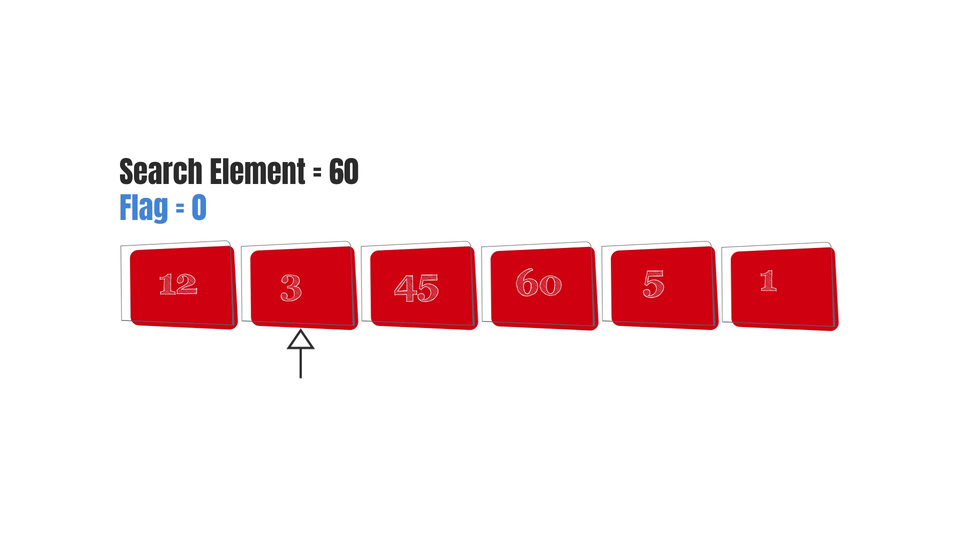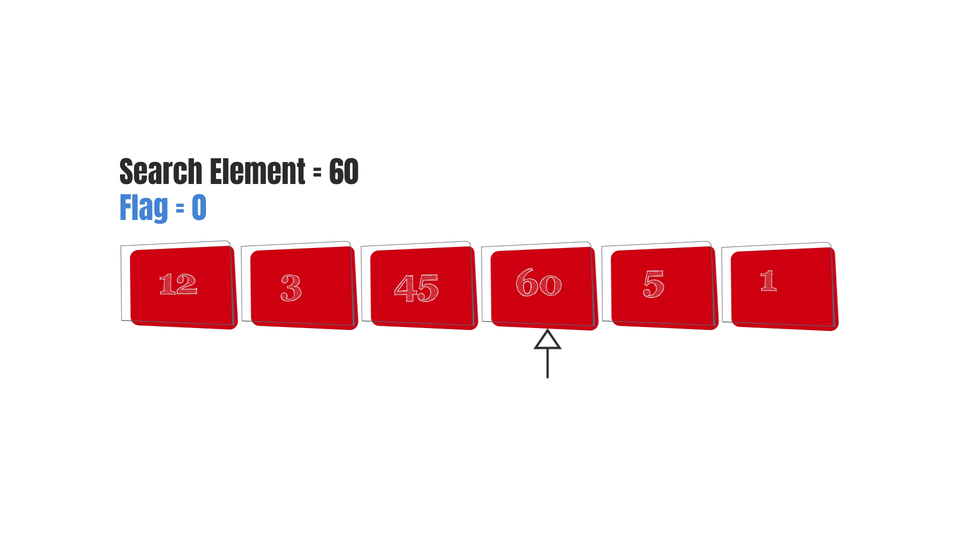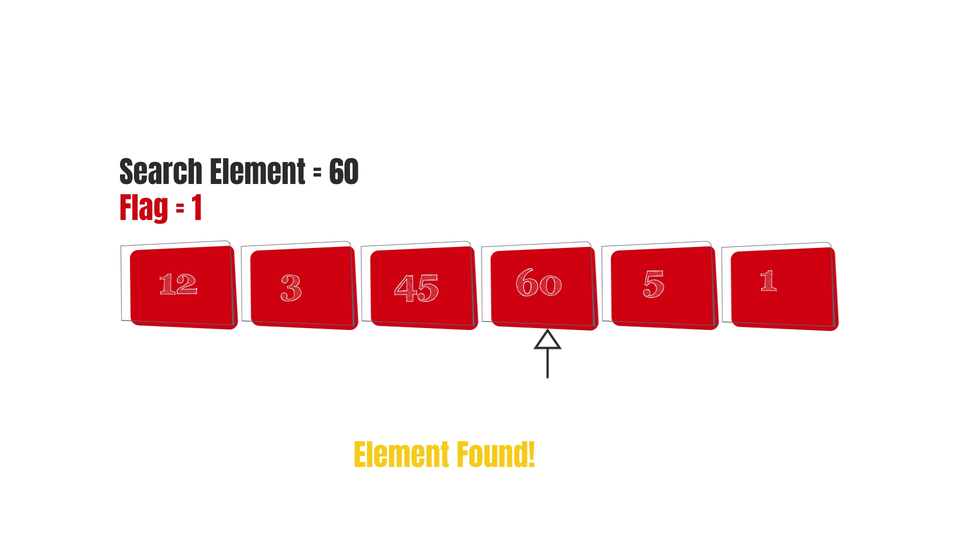 So we can say that it kind of depends on the size of the array. In other words, as the length of the array increases, time taken by the algorithm would increase too. Which means that the complexity of the algorithm is linear, it linearly depends on the size of the array(n).
So we can say that it kind of depends on the size of the array. In other words, as the length of the array increases, time taken by the algorithm would increase too. Which means that the complexity of the algorithm is linear, it linearly depends on the size of the array(n).
In the worst case possible, if the search element is not present in the array-
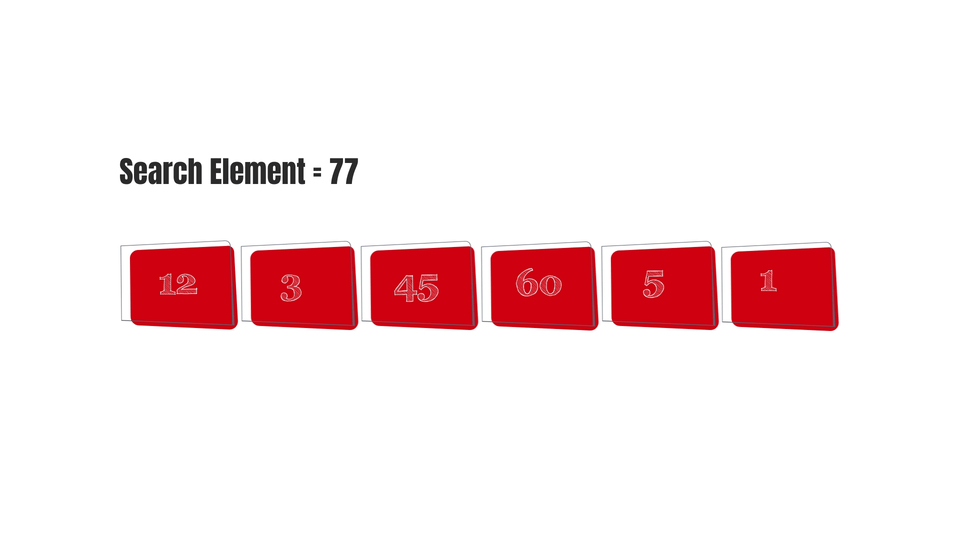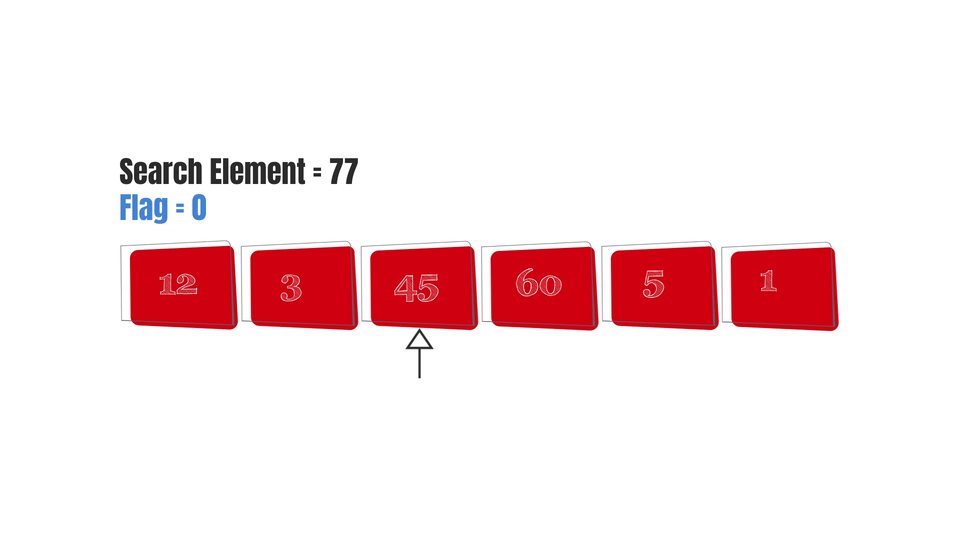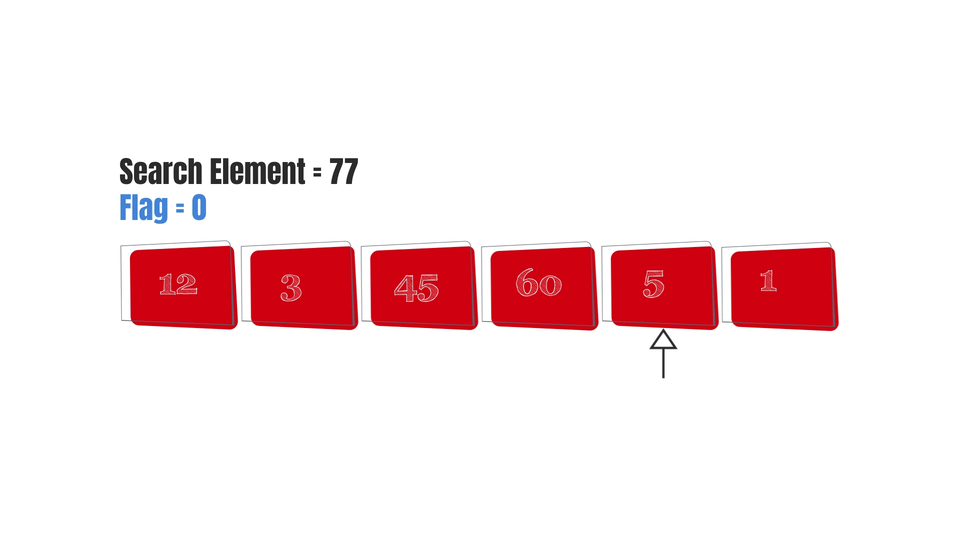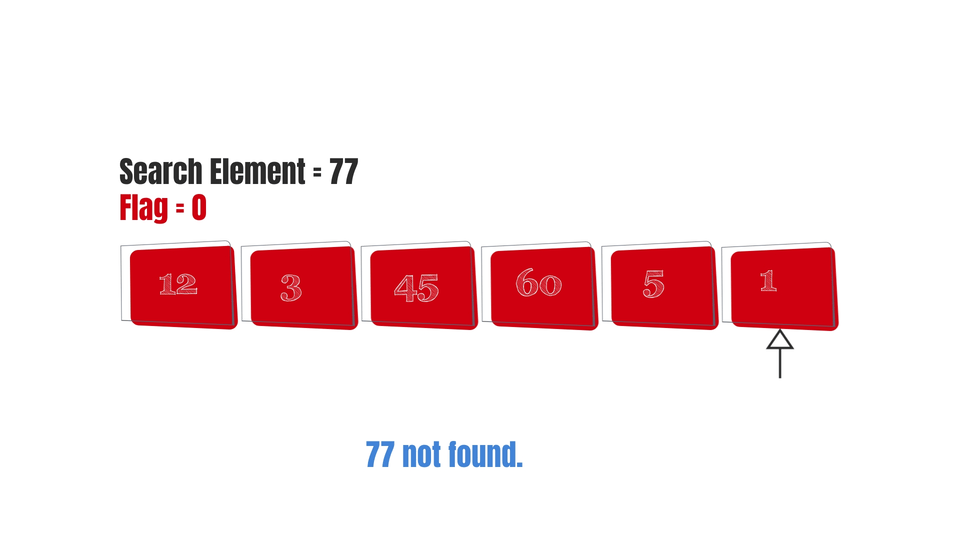 Then the elements present in the array will be visited with no outcome at all.
So, the worst case complexity of Linear Search is O(n).
Then the elements present in the array will be visited with no outcome at all.
So, the worst case complexity of Linear Search is O(n).
Whereas, in Binary Search, all the elements of the array don't have to be visited as the array gets divided in half its size at each step until only one element is left -
 This algorithm doesn't linearly depend on the size of the array. Let's see how we can calculate the time complexity here.
This algorithm doesn't linearly depend on the size of the array. Let's see how we can calculate the time complexity here.
Time Complexity of Binary Search
So, suppose there's an array of length "n".
We perform Binary Search on it, in such a way that -
- In step 1 - length of array = n
- In step 2 - length of array = n/2
- In step 3 - length of array = n/4
- In step 4 - length of array = n/16
and so on.....(k times) where k being a natural number.
Until, length of array = 1
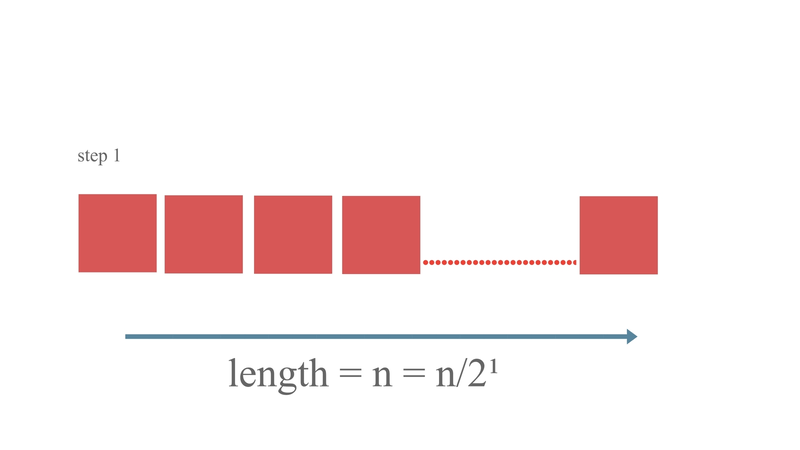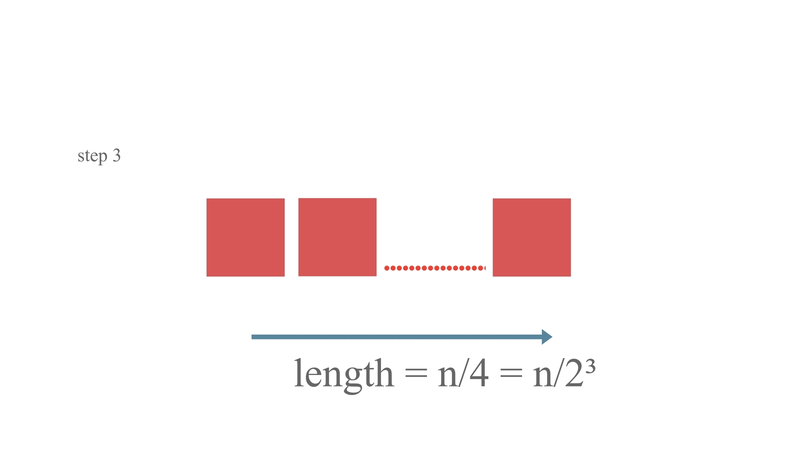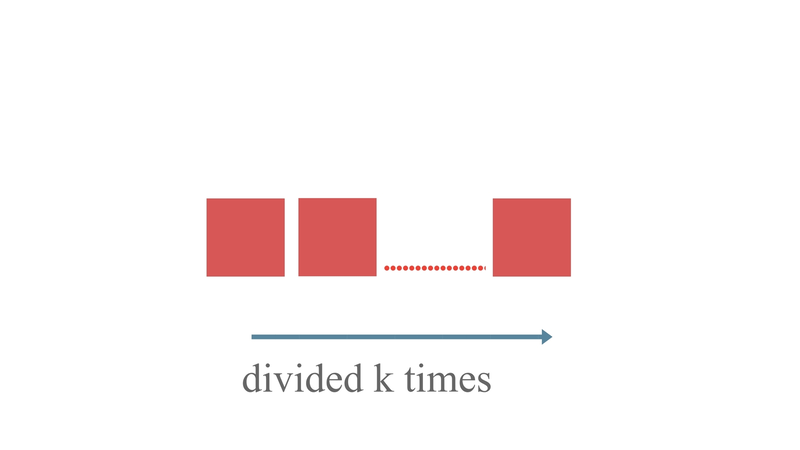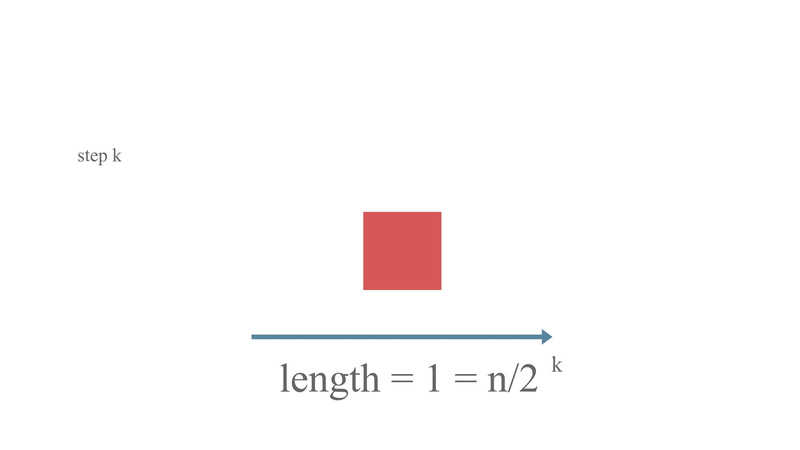 Solving n/2^k = 1, we get -
Solving n/2^k = 1, we get -
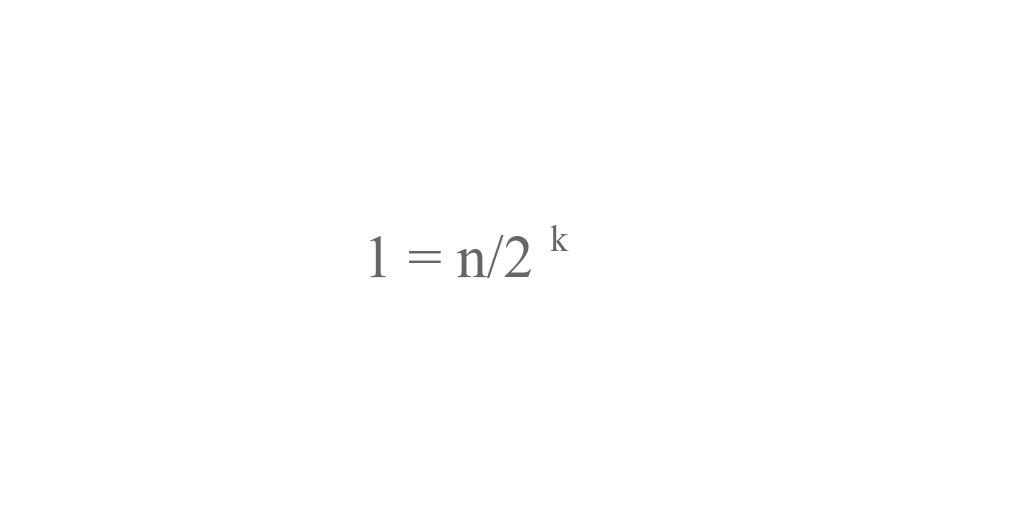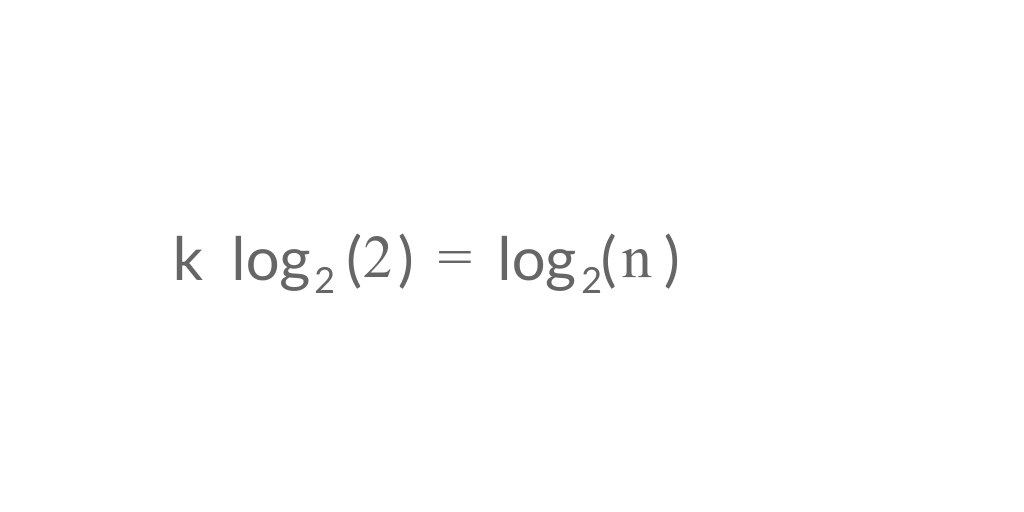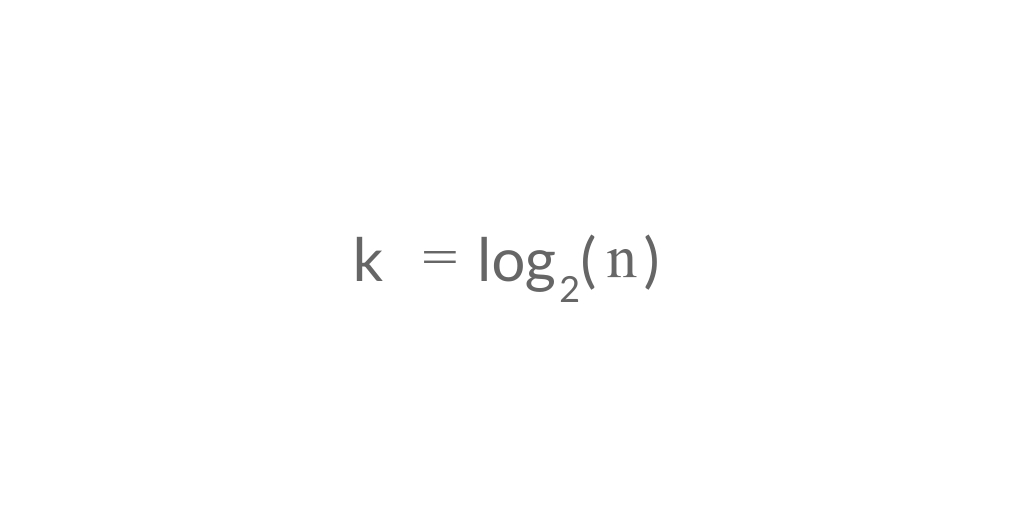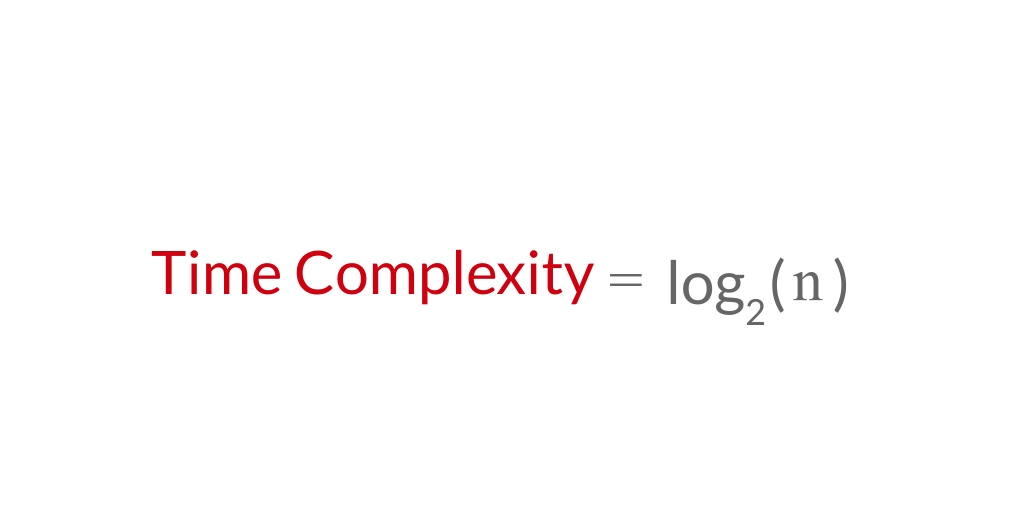 So, the time complexity for binary search is O(log2(n)).
So, the time complexity for binary search is O(log2(n)).
As we already know a complexity of O(log2(n)) is much better than complexity of O(n).
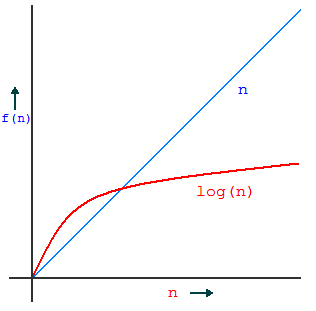
That's why time complexity-wise, Binary Search is preferred over Linear Search.
But both algorithms have their advantages and disadvantages. Like even though linear search is not the most optimized way of searching, it works fine on small arrays and is a simpler approach than binary search. Unlike Binary Search, Linear search can work on unordered array. Binary search cannot be implemented on unsorted arrays but has a better time complexity than linear search.
Conclusion
It basically depends on the type of problem you across to choose which algorithm would be best to use as both have advantages and disadvantages that largely depends upon the test case of the problem. I hope you got a little bit of idea about how you calculate the time complexities of algorithms. Do check out my other posts on Data Structures and Algorithms here.
Thanks for reading! 🎇


