So far we've discussed about insertion, deletion and searching operations in a Binary Search Tree. If you haven't read them yet, you can check them out here. In this post I'm gonna talk about how you can find the K'th - Minimum element in a Binary Search Tree. So, let's start!
What is meant by the "K'th minimum element"
When we want to find the smallest element in an array of elements, we mean to find the element having the least or minimal value among all the other elements present in the array.
Now, if we want to find the 2nd smallest element in the array, we choose the element having a value such that it is greater than the smallest element and at the same time smaller than all the other elements present in the array.
Similarly, by "k'th smallest element" or "k'th minimum element" we mean to find an element which is greater than k-1 elements present in the array which is also smaller than the rest of the elements present in the array.

The Algorithm
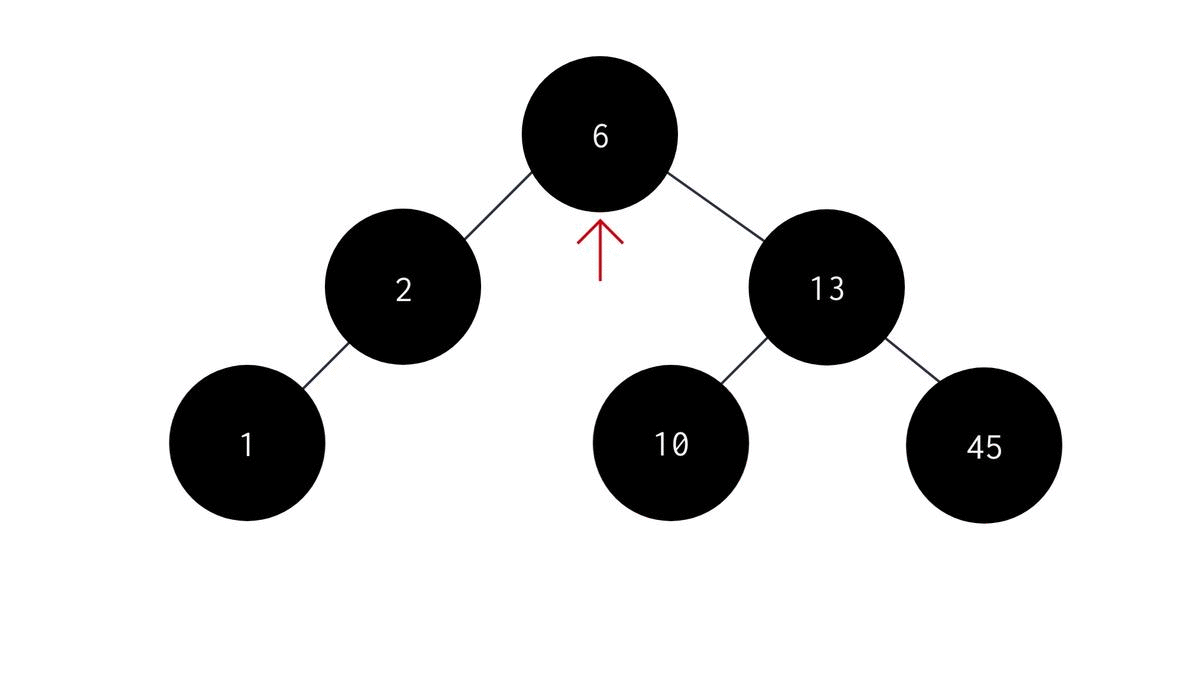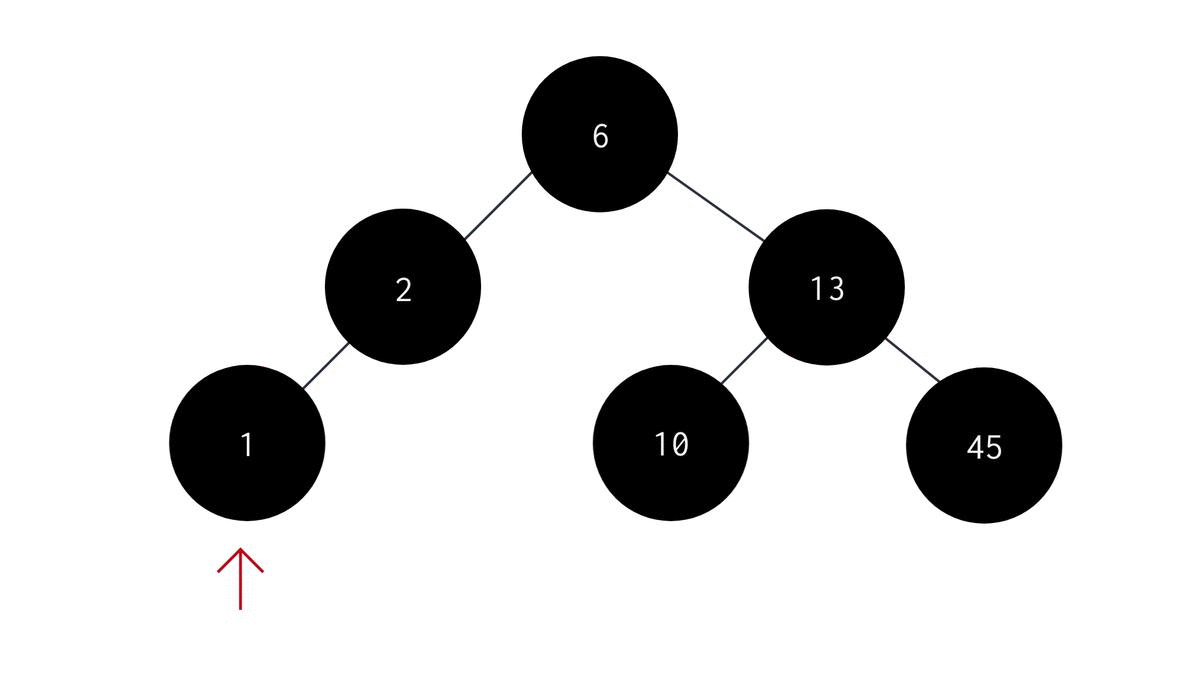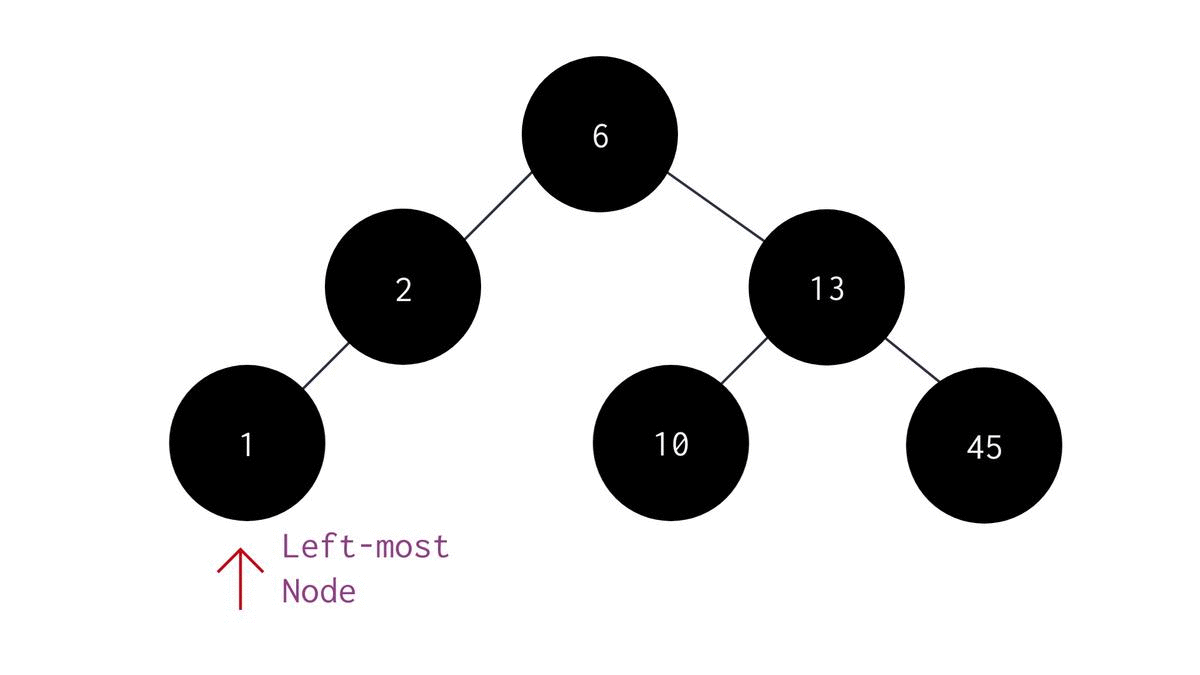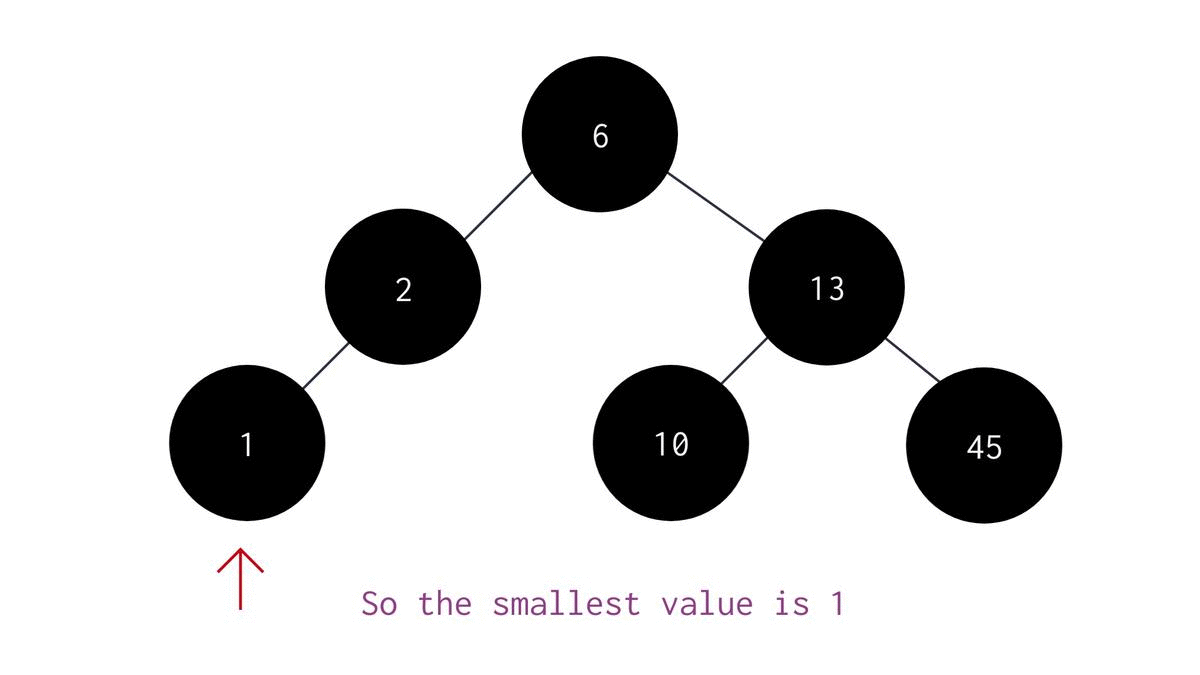
To find the smallest element in a Binary Search Tree, you can simply return the left-most element of the tree. It can be done like this -
- Start from the root node as the parent node.
- Traverse through the tree such that -
- You move to the left of parent node.
- Keep moving until the left child is equal to NULL.
- Return the data of the node where the pointer points at finally. The code would look something like this :
int smallestelement(NODE *root){
if(root == NULL){
return root->data;
}else{
NODE *temp = root;
while(temp->left != NULL){
temp = temp->left;
}//temp reaches the left-most node;
return temp->data;
}
}
But, finding the K'th minimum value is a little more complicated than this as you'll have to keep track of the number of nodes you've visited in the inorder fashion until you reach the K'th element in in-order arrangement. That's why, we're gonna use a counter variable to solve this problem.
Another issue with this problem is that we cant be sure if the K'th minimum is definitely gonna be in the left subtree unlike the smallest element problem. To make you understand that better, lets look at an example -
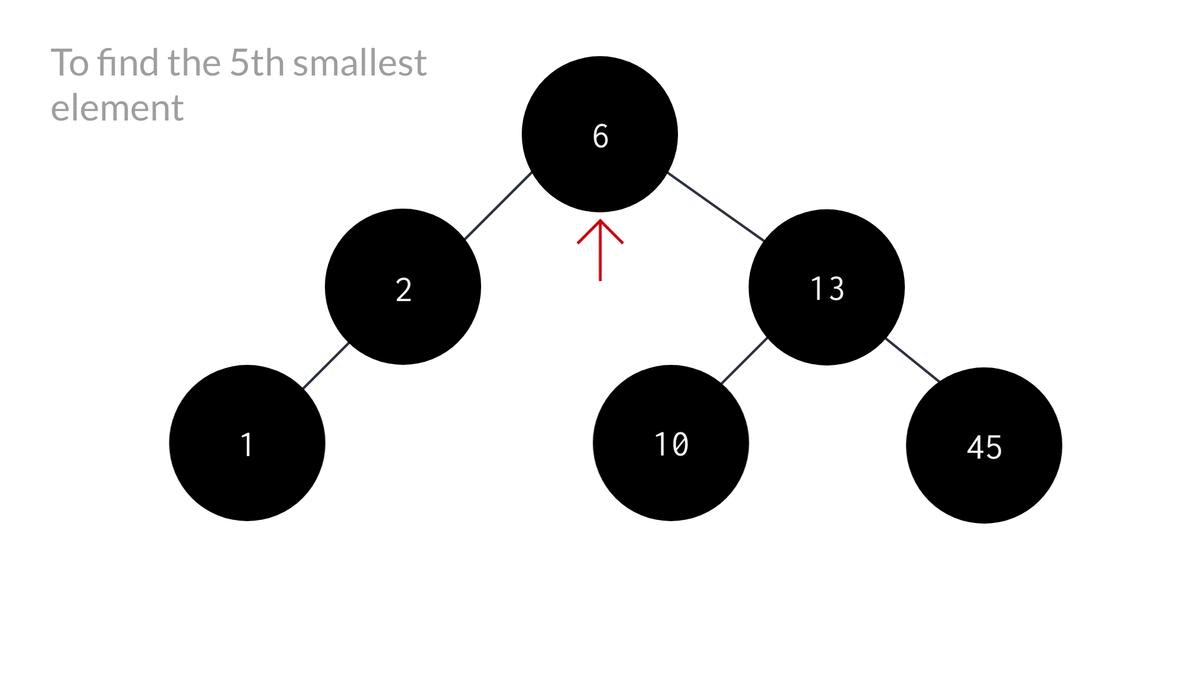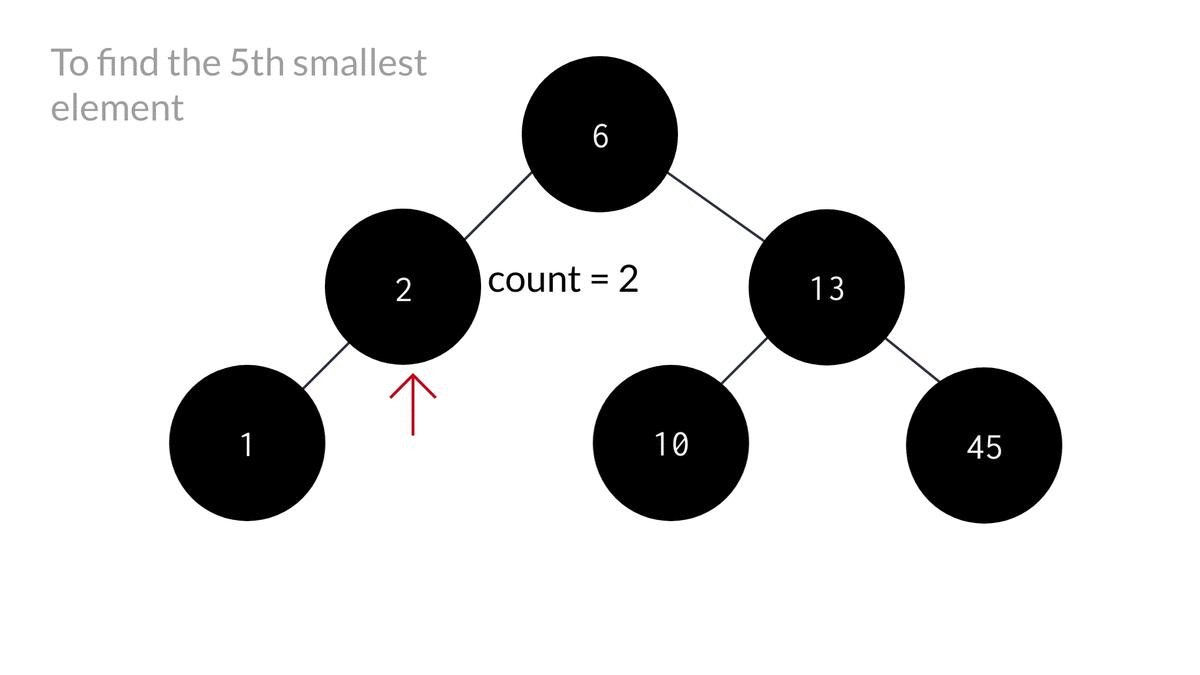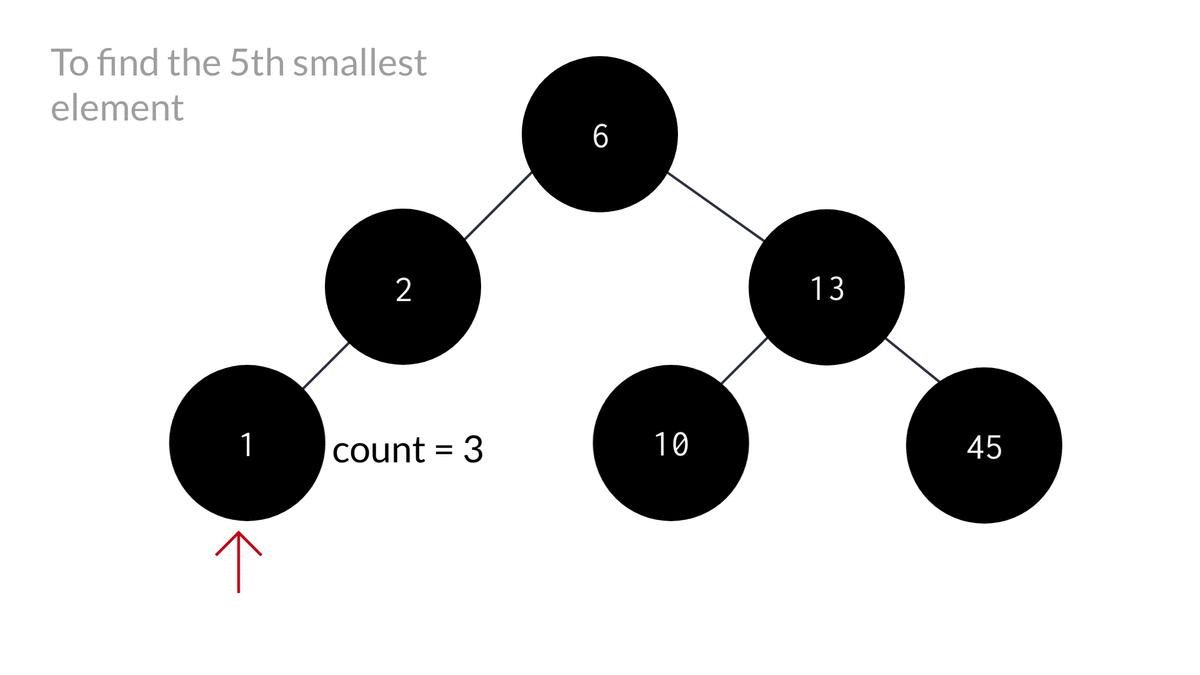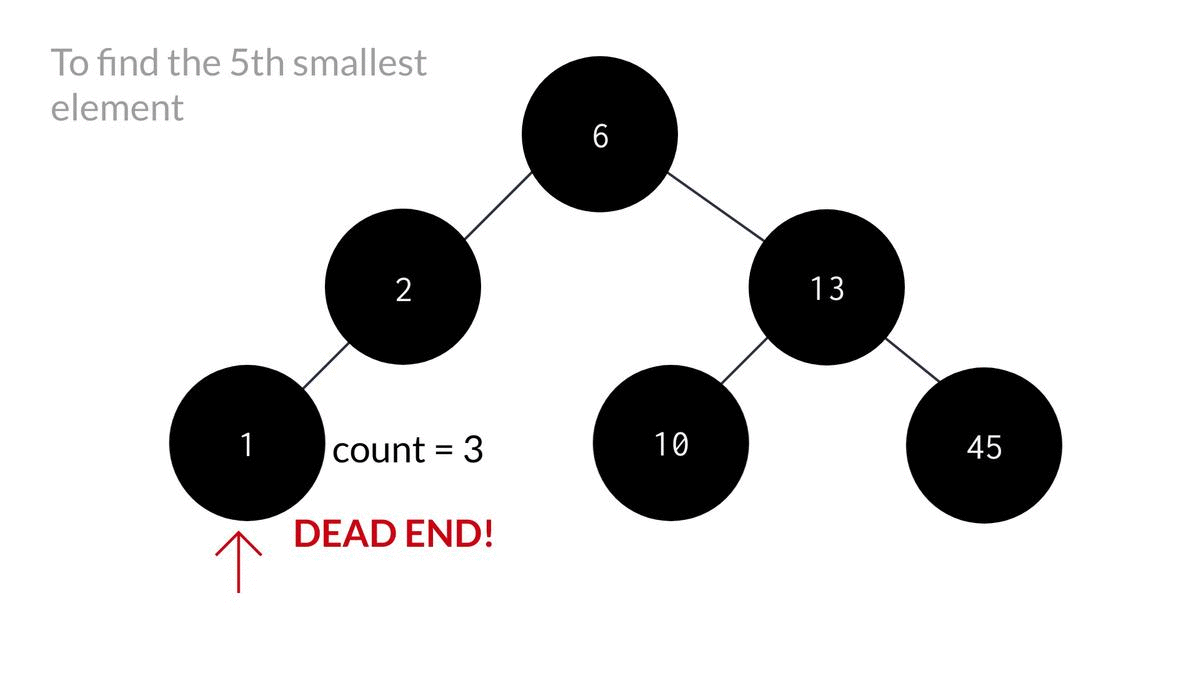 As you can see, blindly traversing to the left subtree would lead us no where in finding the k'th minimum.
So, in our algorithm, we'll first check the left subtree and if the element is not found, we'll move on to the right one.
So, the algorithm looks something like this:
As you can see, blindly traversing to the left subtree would lead us no where in finding the k'th minimum.
So, in our algorithm, we'll first check the left subtree and if the element is not found, we'll move on to the right one.
So, the algorithm looks something like this:
- Start from the root node as the parent node.
- Check if parent node is NULL or if count is greater than k. If so, then return nothing. Else do the following:
- Start with the left subtree, so that we can reach the smallest node first.
- Increase the count by 1.
- Check if count is equal to k or not. If it is, print the data of the current parent node as that would be the k'th smallest. Else:
- Recursively call the same function until k'th min is found or current node becomes NULL.
- If k'th min was not found in the left subtree, perform recursion on the right subtree.
The code for the same looks like this -
void kthSmallest(NODE* root, int *count, int k)
{
if(root == NULL || (*count) >= k){
return;
}
//smallest element in visited first
kthSmallest(root->left, count, k);
(*count)++; // increase the count of visisted nodes
if(*count == k){ // if count is equal to k, then k'th min is reached.
printf("K'th smallest value is %d\n", root->data);
}
//recursion for right subtree
kthSmallest(root->right, count, k);
}
void kthSmallestElement(NODE *root, int k){
int count = 0;
//passing "count" by reference
kthSmallest(root, &count, k);
}
Here, I've used another function to pass the value of count by reference as we can't simply change the value of a variable located outside of a function from within the function. We can only do so by accessing the variable through it's address in the computer's memory which is also called "calling by reference".
Alright, so now that we're done with the coding part, Let's look at a clearer representation of the code for a better understanding.
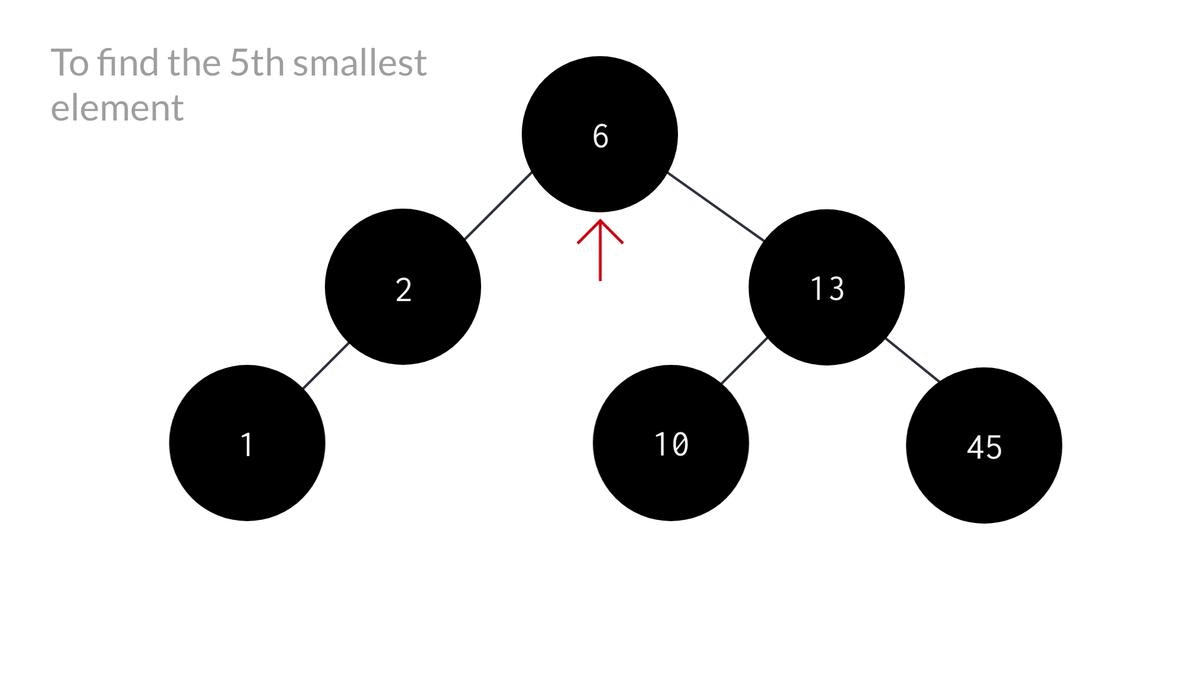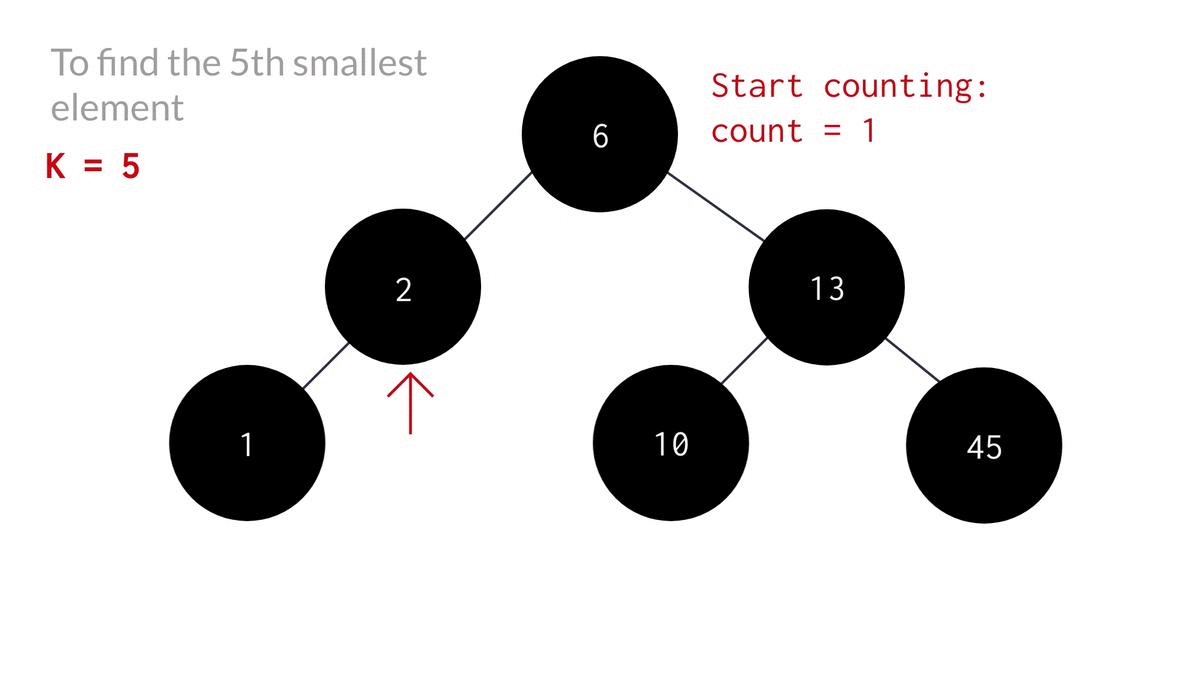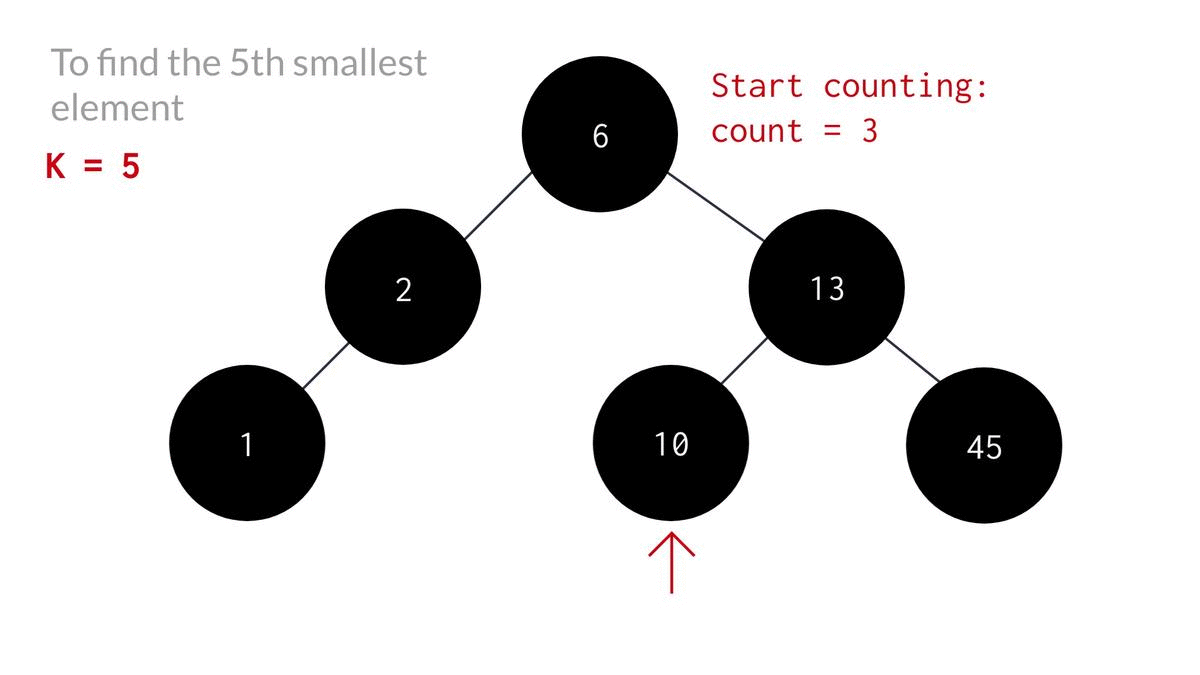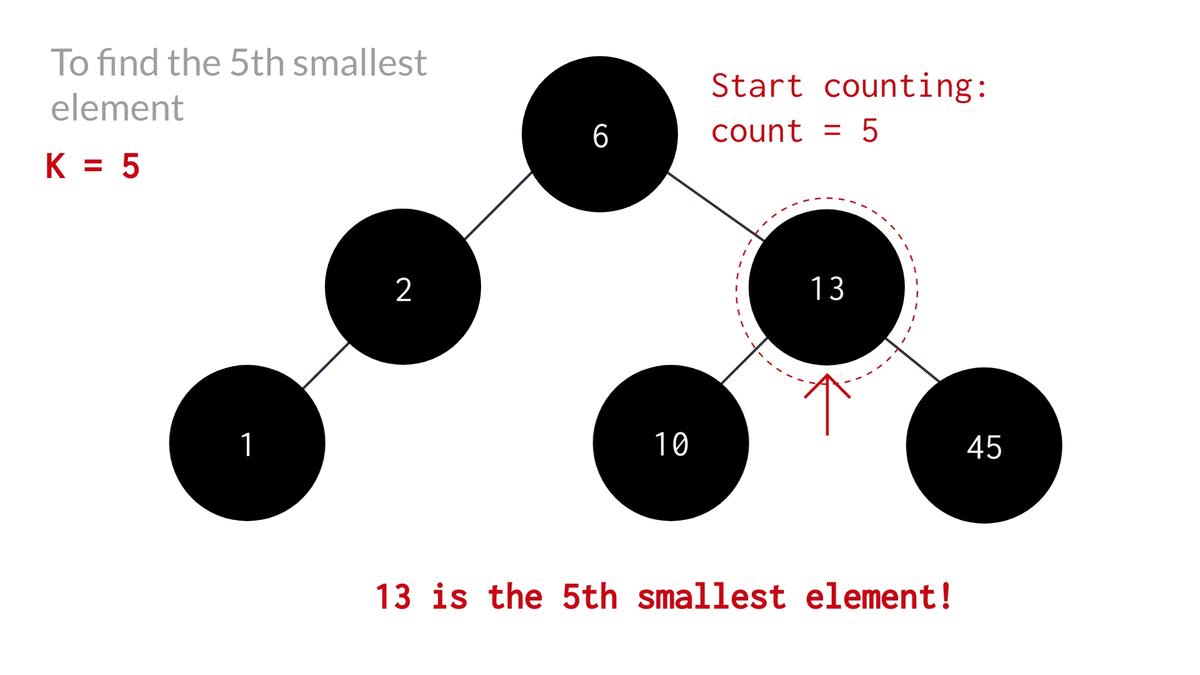
We can also do it by traversing the tree in inorder fashion and storing them in an array and then printing the k'th element of the array.
Conclusion
This whole method of finding the k'th minimum element is based on keeping track of the nodes visited while doing inorder traversal of the tree.
There can be many other methods for doing the same, but I found this method more complex than the others when I first came across it. So this was my attempt to present this topic in the easiest way possible.
Hope you liked reading this article. You can check out my other articles here. Thanks for reading!


