K'th maximum element in a Binary Search Tree

In this article I'm gonna talk about how we can find the k'th maximum element in a given Binary Search Tree.

Previously we talked about the methods of finding the k'th minimum element in a BST. If you haven't read that yet, please check it out here because we're gonna use the similar concepts here.

In k'th minimum element search, the main idea we used was - Inorder traversal of the BST while maintaining a counter variable to keep track of the number of elements we visited at each step. Here, we're going to do the same thing, but with a slight difference. The difference is - do the opposite of inorder traversal. That means, instead of visiting nodes in L(left child), D(current node), R(right child) sequence, we'll be traversing it in R, D, L sequence.

So, instead of visiting the left subtree of the root node first, we'll be visiting right subtree first.

Algorithm

The algorithm therefore, would be of this sort -

1. Start with the root node as parent node.
2. check if parent node is NULL or count is greater than k. If so, return nothing. Else, do the following -
3. Start with the right subtree so that we can reach the largest element first.
4. Increase the count by 1.
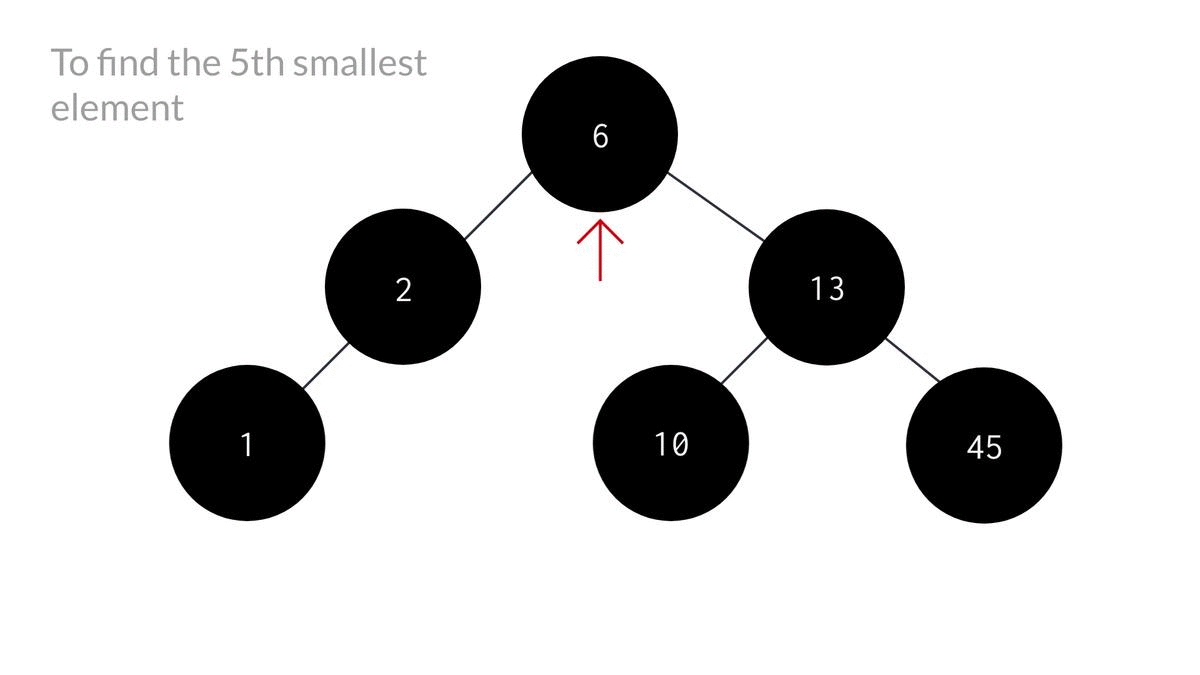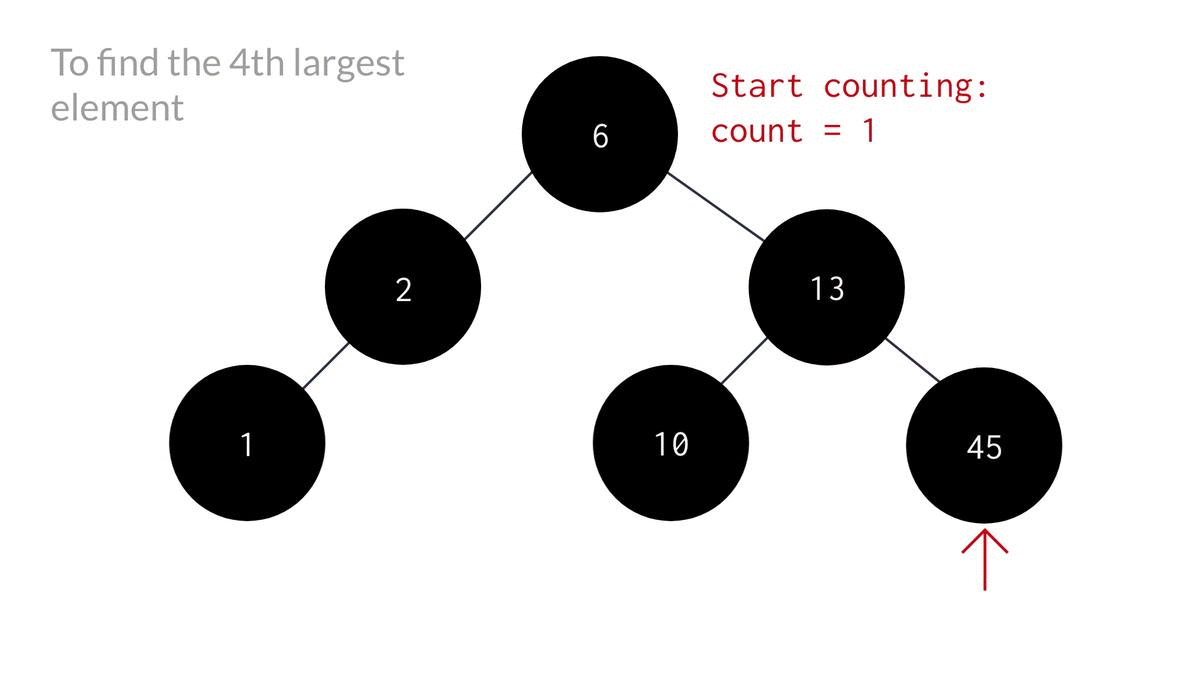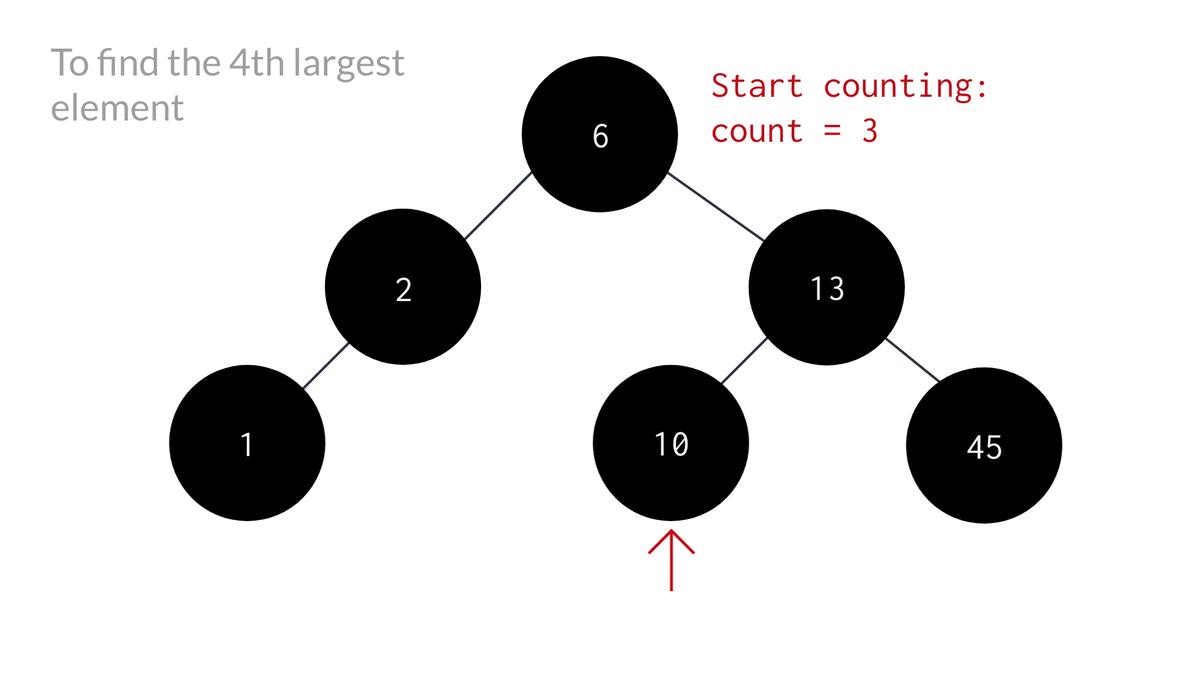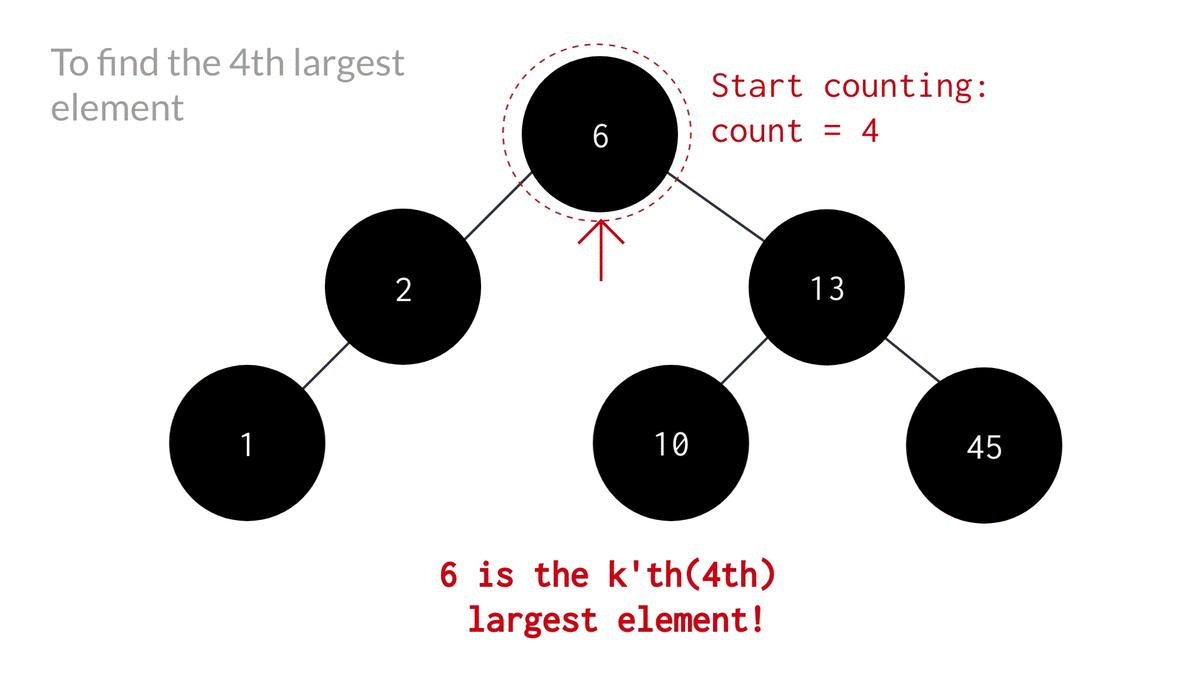
5. Check if count is equal to k or not. If it is, print the data of the current node as that's the k'th maximum element. Else:
6. Recursively call the same function until k'th max element is found or current node becomes NULL.
7. If k'th max was not found in the right subtree, perform recursion on the left subtree.

Code

The C code for the same is:

void kthLargest(NODE* root, int *count, int k)
{
    if(root == NULL || (*count) >= k){
        return;
    }
    
    //largest element is visited first
    kthLargest(root->right, count, k);
    (*count)++; // increase the count of visited nodes
    
    if(*count == k){ // if count is equal to k, then k'th max is reached.
        printf("K'th smallest value is %d\n", root->data);
    }
    
    //recursion for right subtree
    kthLargest(root->left, count, k);
}

void kthLargestElement(NODE *root, int k){
    int count = 0;
    
    //passing "count" by reference
    kthLargest(root, &count, k);
}

Note that this whole code has the exact opposite idea of what we did to find the k'th min element in a BST.

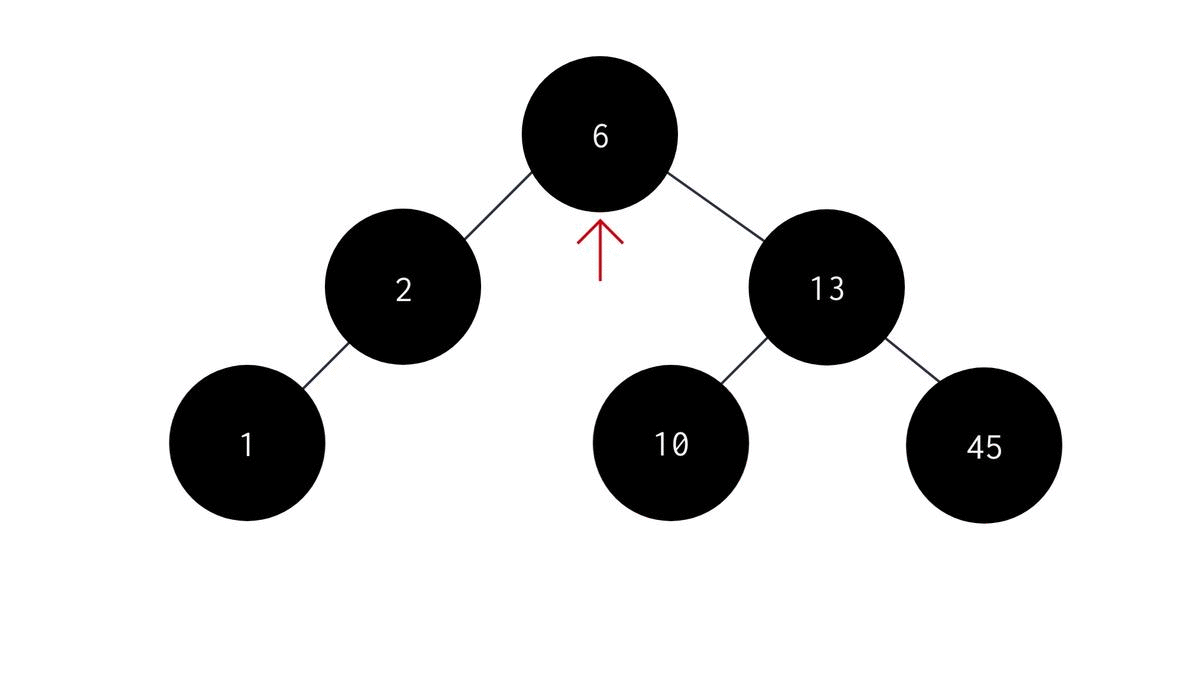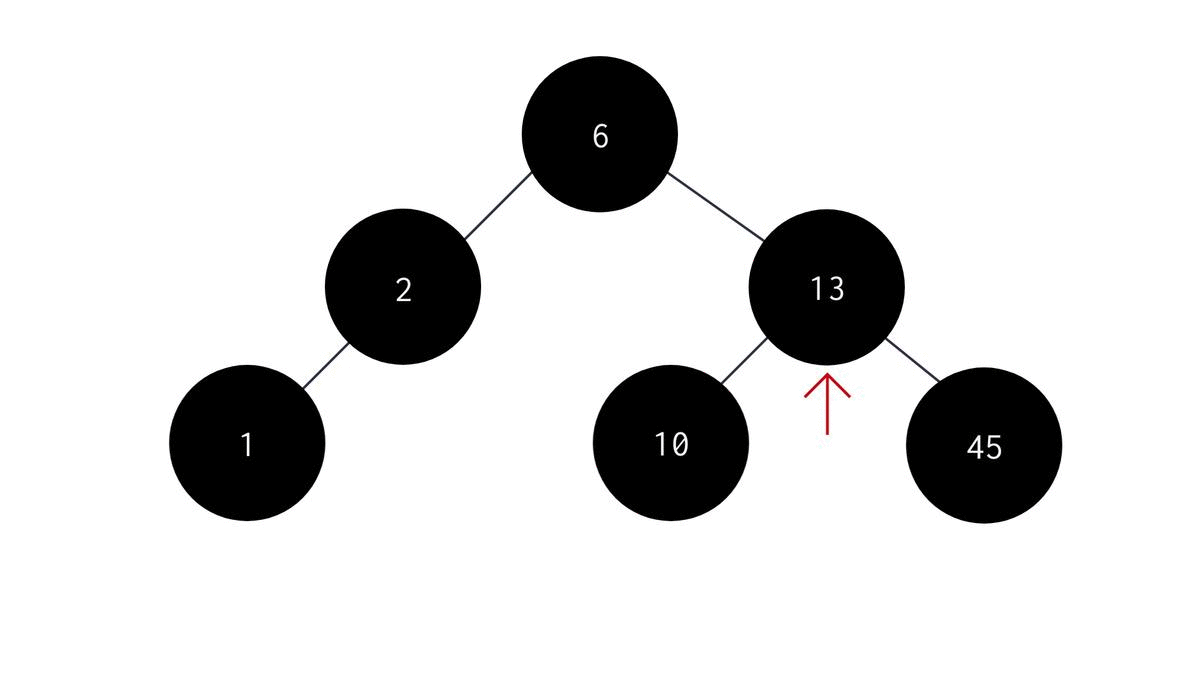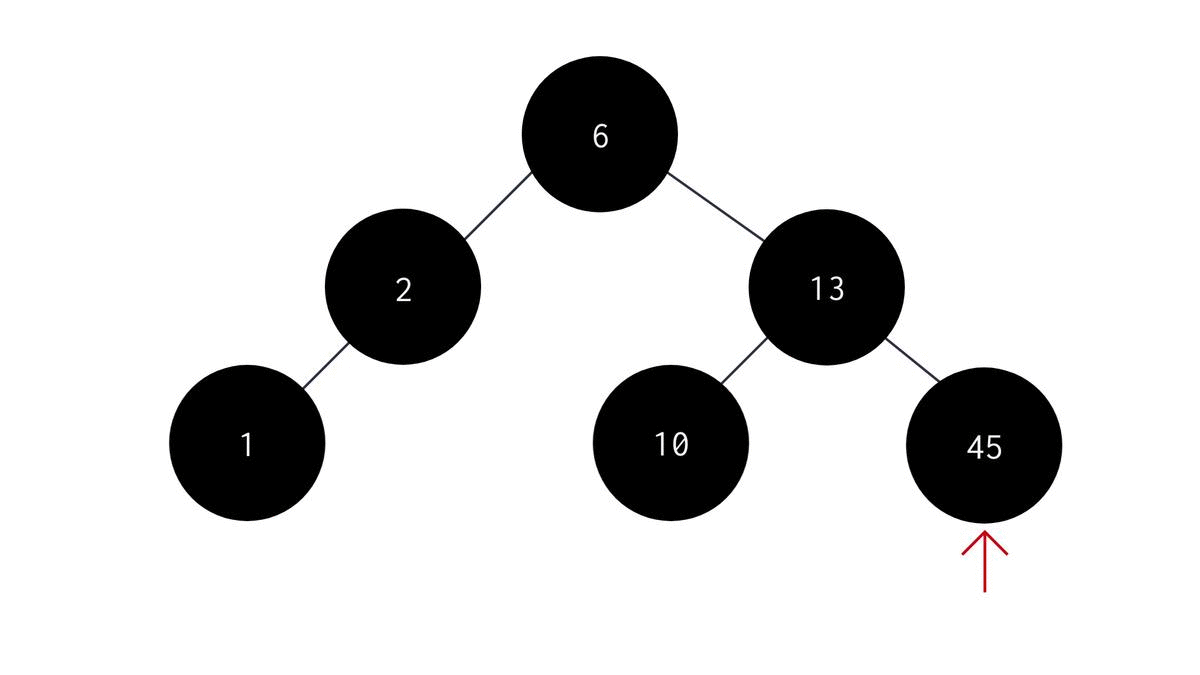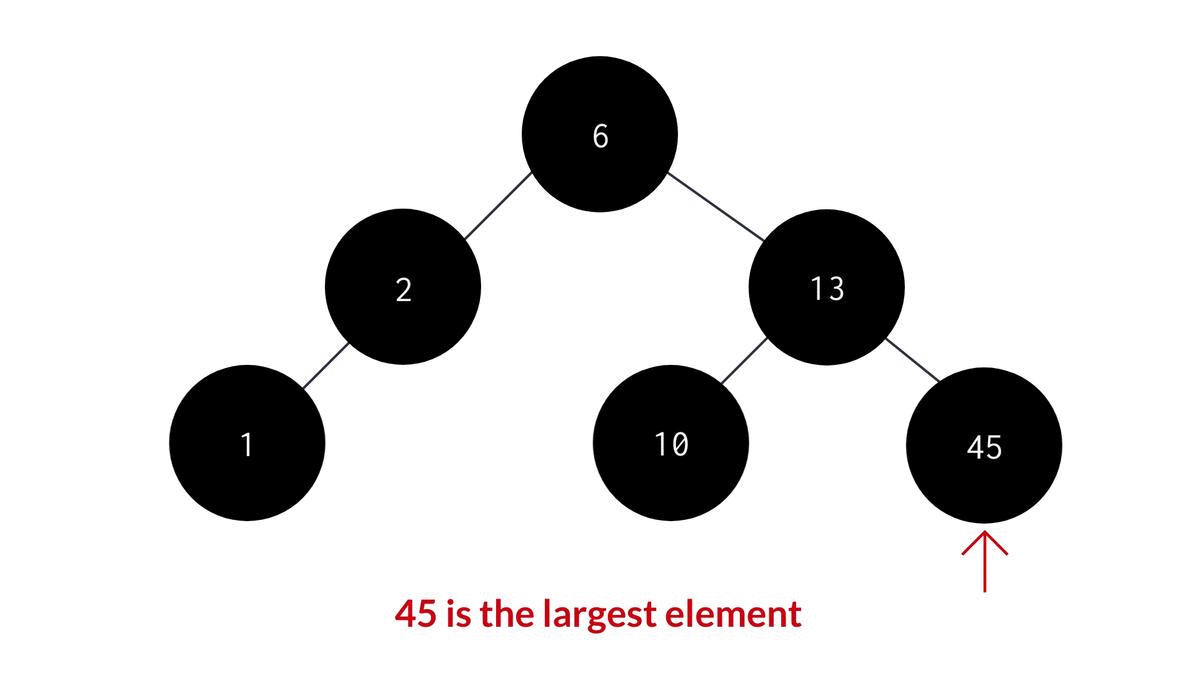
Maximum element in a BST

Similarly, you can find the maximum element in a BST by doing the exact opposite of what we did to find the smallest element in a BST. You just have to switch left subtree with right subtree. The code would therefore look like this -

int largestelement(NODE *root){
    if(root == NULL){
        return root->data;
    }else{
        NODE *temp = root;
        while(temp->right != NULL){
            temp = temp->right;
        }//temp reaches the left-most node;
        return temp->data;
    }
}

Conclusion

The same problem could've been solved by doing the opposite of inorder traversal and storing each element in an array and then later finding the k'th element of that array. Probably that would've looked like an easier method to you, but the time complexity for both the methods are same.

I found this method a little tricky at first so I've done the best to break it down and illustrate it in the best way possible.

This is it for this article. I hope you liked reading it. You can read more such articles here

Thanks for reading!