Insertion Sort

Insertion sort is a technique of sorting wherein you build a sorted array from an unsorted one by picking wrongly placed elements from the unsorted part of the array and placing them at the correct position in the sorted part.

What is insertion sort?

In this technique of sorting, we basically select an element of the array at a time and compare it with its predecessor. Swapping is done based on the order in which we have to arrange the elements(ascending or descending).

So, we build a sorted array from an unsorted one by repeatedly comparing and swapping each element with its predecessor.

Example

Suppose that you work in a clothing shop. You are given this task to arrange some shirts in increasing order of their sizes. How would you do that?

The best technique for a sorting of this kind involves the use of Insertion Sort. You'll go through all shirts from left to right, one by one. Compare the current shirt with the one before it and place it accordingly. The process might look something like this -

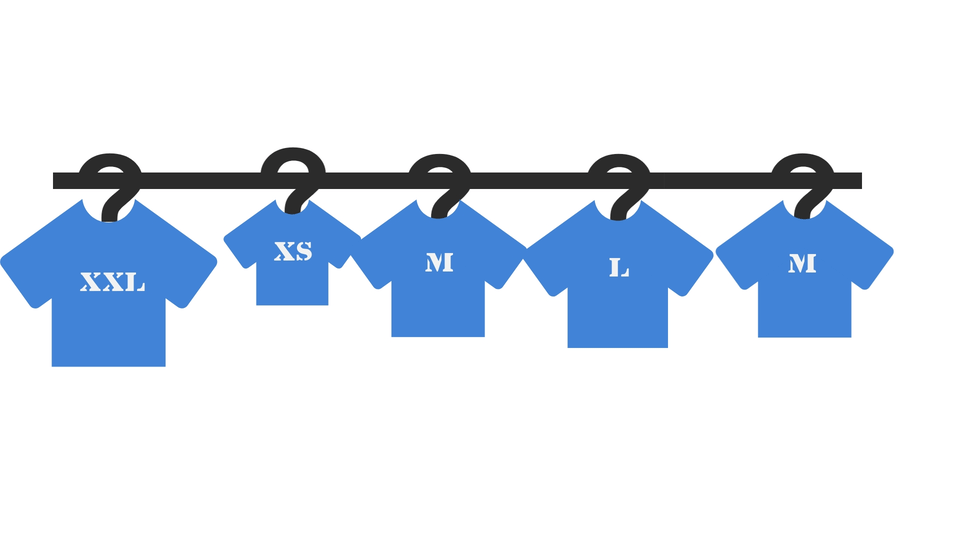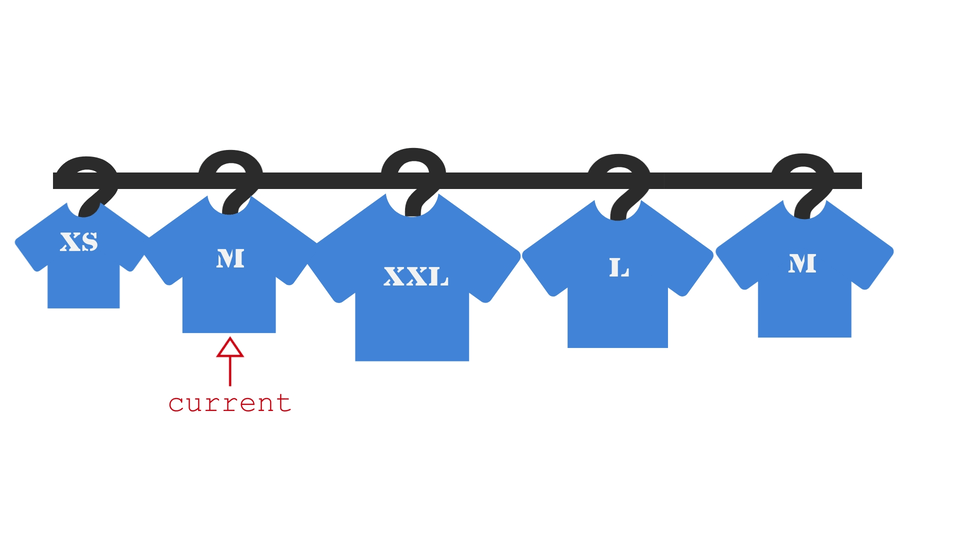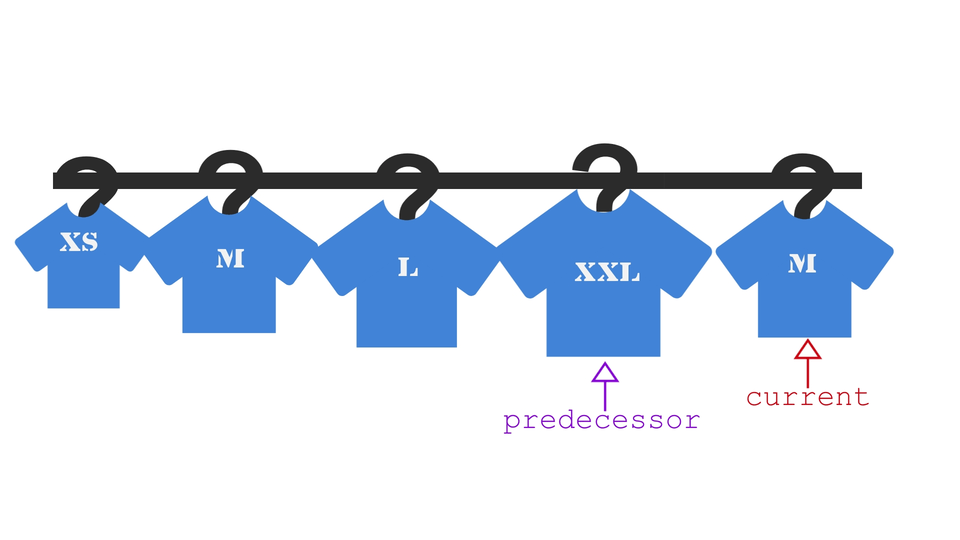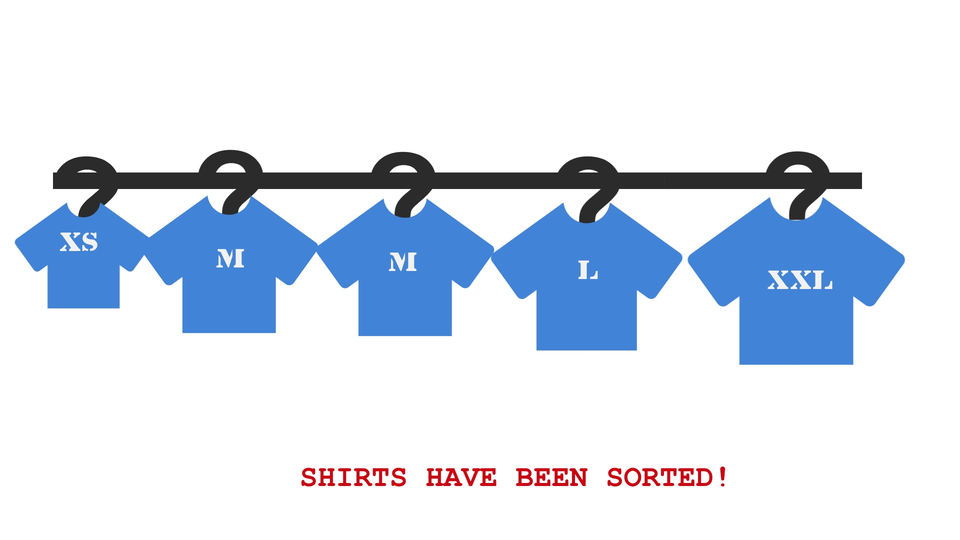
The Algorithm

In this sorting algorithm all we do is -

1. pick each element from the array one by one. We'll call this element "Current" element.
2. now compare the current element(element at i'th index) with its predecessor(element at i-1'th element). If -
   1. it is greater than current, swap the two.
   2. Otherwise, do nothing.
3. Repeat step 2 again and again until the predecessor is some element smaller than the current element.
4. Repeat steps 1 to 3 for all elements present in the array, one by one.

An illustration to clarify the concept -

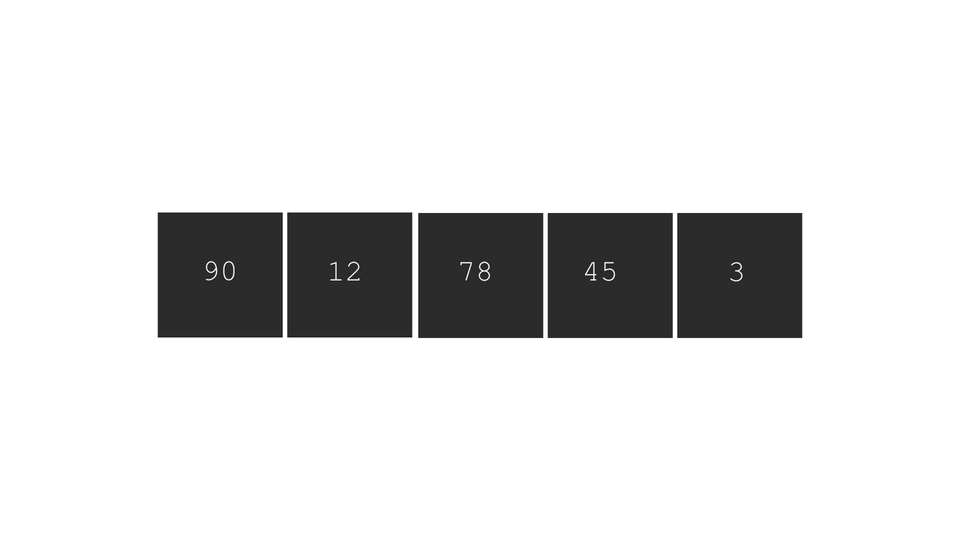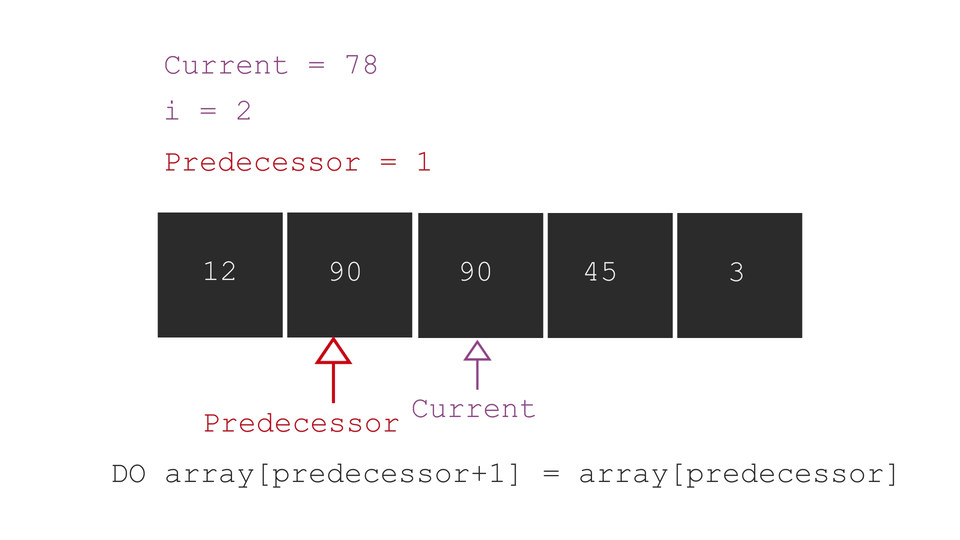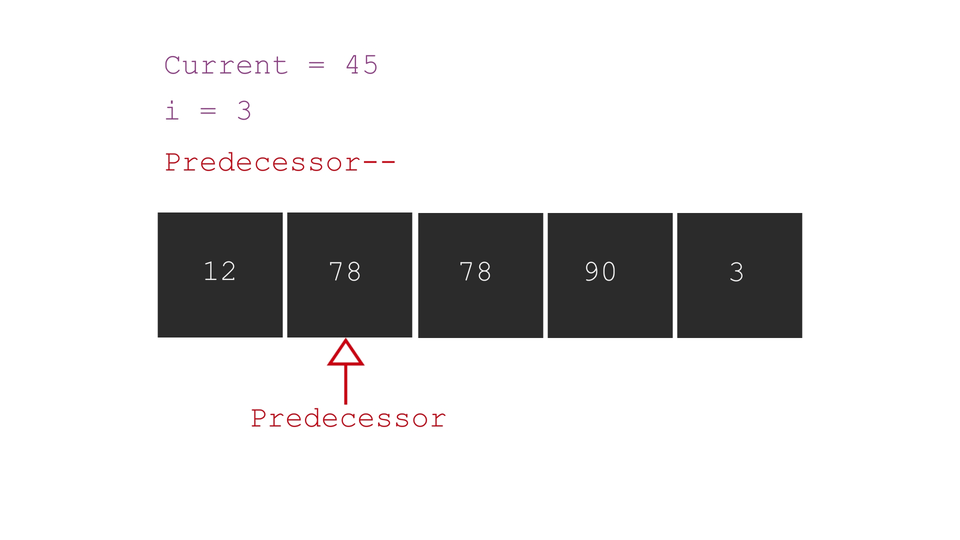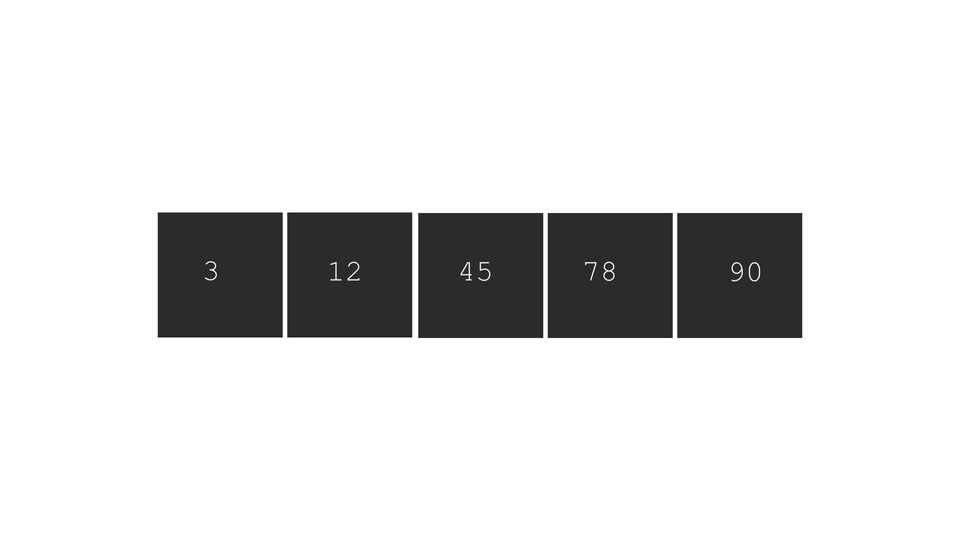
Note that these steps must be followed only if you want to arrange the array in ascending order. For sorting in descending order, flip the comparison conditions.

Code

You can use the following C code to implement insertion sort algorithm on a user entered array -

void insertion_sort(int n, int *arr){
    int current, predecessor;
    for(int i=1; i<n; i++){
        current = arr[i];
        predecessor = i-1;
        while(arr[predecessor] > current && predecessor>=0){
            arr[predecessor+1] = arr[predecessor];
            predecessor--;
        }
        arr[predecessor+1] = current;
    }
    print_array(n, arr);
}

Again, note that the above code will work for arranging the numbers in ascending order. To arrange in descending order, flip the comparison condition.

The full code for the same is-

#include <stdio.h>

void print_array(int n, int *arr){
    for(int i=0; i<n; i++){
        printf("%d ",arr[i]);
    }printf("\n");
}

void insertion_sort(int n, int *arr){
    int current, predecessor;
    for(int i=1; i<n; i++){
        current = arr[i];
        predecessor = i-1;
        while(arr[predecessor] > current && predecessor>=0){
            arr[predecessor+1] = arr[predecessor];
            predecessor--;
        }
        arr[predecessor+1] = current;
    }
}

int main(){
    int n;
    printf("Enter size of the array: ");
    scanf(" %d", &n);
    
    int arr[n];
    printf("Enter the elements of the array\n");
    for(int i=0; i<n; i++){
        printf("Enter element: ");
        scanf(" %d", &arr[i]);
    }
    
    printf("UNSORTED ARRAY: ");
    print_array(n, arr);
    
    //apply insertion sort
    insertion_sort(n, arr);
    
}

Conclusion

Personally, I found insertion a bit thicker to understand than the previously learnt sorting methods. But it is faster than Bubble and Selection sort and works comparatively better if you want to sort a small sized array. I hope I made the concept of this algorithm a little bit clearer for you. You can find more such articles here.

Thanks for reading!🎆