Divide and conquer is just a simple yet complex strategy of solving problems. It basically includes the idea of dividing a problem into sub-problems or smaller problems. We solve each sub-problem one by one until all the sub-problems are solved.
This strategy is useful when you're given a task of solving a bigger problem with higher complexity. You can just substitute that big problem into smaller and simpler sub-problems and then solve each of them one by one.
Steps
This strategy usually consists of 3 steps-
- Divide the problem as much as possible,
- Solve the problem,
- And finally, Combine the result of all the sub-problems to produce the result of the main problem that was given.
An Example
Suppose that you're really hungry and you wanna prepare a sandwich for yourself. How would you prepare it? It is obviously gonna include some simple steps like getting the ingredients, cooking them up, stuffing them inside the bread and so on. isn't it? The combined effort that you invest in all these steps would finally result in a sandwich at the end.
In a similar way, you get a problem, you divide it into smaller steps and then combine them all up one by one in the right order to get the required end result. That's what Divide and Conquer Algorithm is all about.
How to implement?
The divide and conquer strategy is used in many algorithms. Usually, recursions are used to divide the problems and combine the sub-problems.
Suppose that we're applying Divide and Conquer strategy to sort an array. In this case, the array of numbers that we have to sort would be considered as the big problem. So, the steps that we can follow could be -
- Dividing the given array of numbers into smaller arrays(an array containing only a single element).
- Solving would include, checking which array contains element greater than another array.
- Combining the array based on the result of step-2 i.e, if sorting is done in ascending order, merge such that the array which contains element smaller than the other array come before that array.
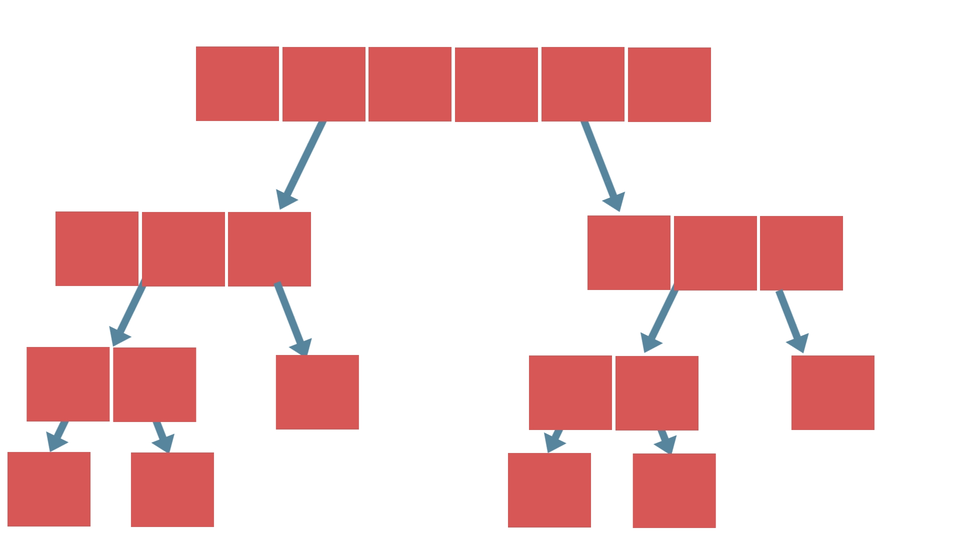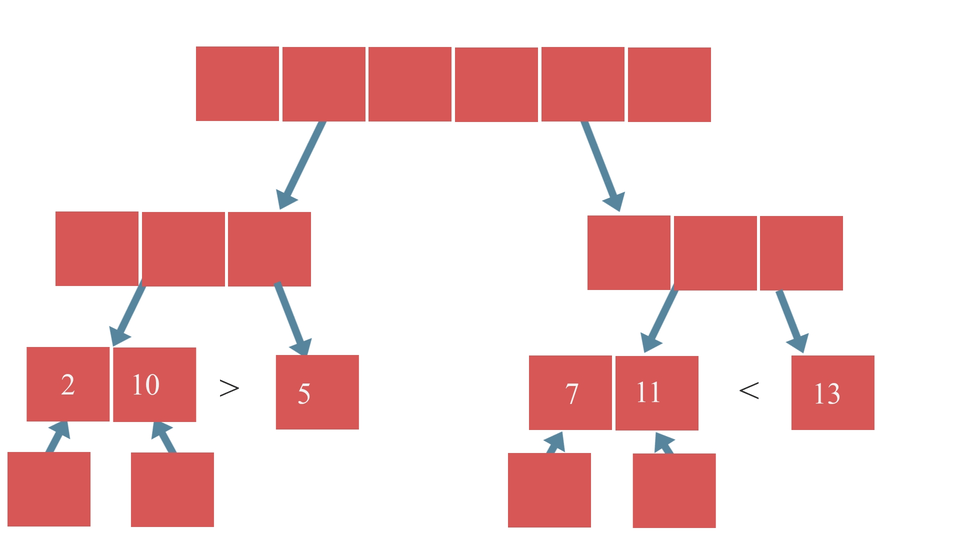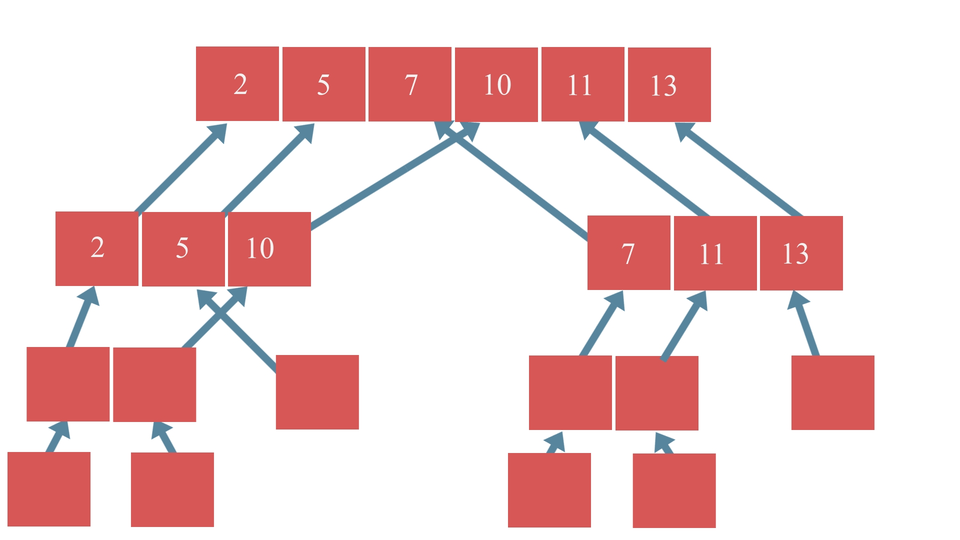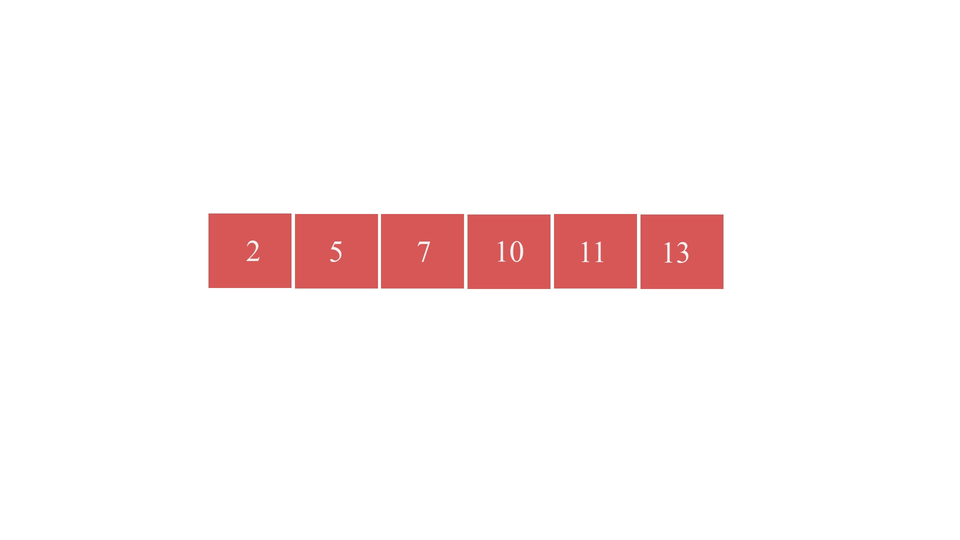The type of sorting that we defined just now is called The Merge Sort. It is faster than the other sorting algorithms like Bubble Sort or Insertion Sort as this algorithm doesn't iterate over the whole array as we can see. Therefore it is considered to be efficient when applied on larger arrays.
Complexity
The complexity of algorithms that use this kind of strategy is usually calculated with the help of Master's theorem.
Advantages
- Difficult problems can be solved with an easier approach.
- Algorithms that are made using this strategy are mostly found to be really efficient.
- Supports parallelism which makes it faster.
- Makes an efficient use of memory cache. As the sub-problems become simpler, they can be solved within the cache memory easily and there's no need to access the main memory which is comparatively slower.
Disadvantages
Recursions are considered to be slow, which is one of the main problems with this strategy. Also, sometimes using this approach is not quite beneficial as it makes the problem more complicated than easier, for instance - when we start using it at situations where we could've simply used iterative method. Recursions over-complicated the problem at such situations.
Applications
Some important applications of Divide and Conquer can be observed in sorting algorithms like - Merge Sort and QuickSort. Strassen's algorithm for Matrix multiplication also makes use of it. Usually we find its application in problems that can be broken down and merged easily.
Conclusion
This was all about the Divide and Conquer Strategy of problem solving. I hope you liked reading this article. You can find more such articles here.
Thanks for reading!🎍