Asymptotic Notations

Previously, we briefly discussed about time complexity of algorithms. You can check it out here if you haven't yet.

In this post we'll learn about the concept of time complexity in a more detailed way. A mathematical way of representing the time complexity of an algorithm. It's definitely gonna include some uncomfortable looking mathematical equations. But don't worry yet! This post is gonna make things easier for you.

So, Let's get started!

What are Asymptotic Notations?

An Asymptotic Notations is the notation which represent the complexity of an algorithm.

It is used to study how the running time of an algorithm grows as the value of the input or the unknown variable increases. Therefore, it is also known as the "growth rate" of an alogrithm.

Meaning of Asymptote

Now, you might wonder what "asymptotic" means here. Right?

The term "asymptote" was coined by the Greeks and it means "not falling together".

Now suppose there's a line and a curve. Both the figures are extended infinitely in such a way that it seems like they might intersect at some point. But they never intersect. The line in such a scenario would be called an "Asymptote" of that curve. But that's the general meaning of an Asymptote.

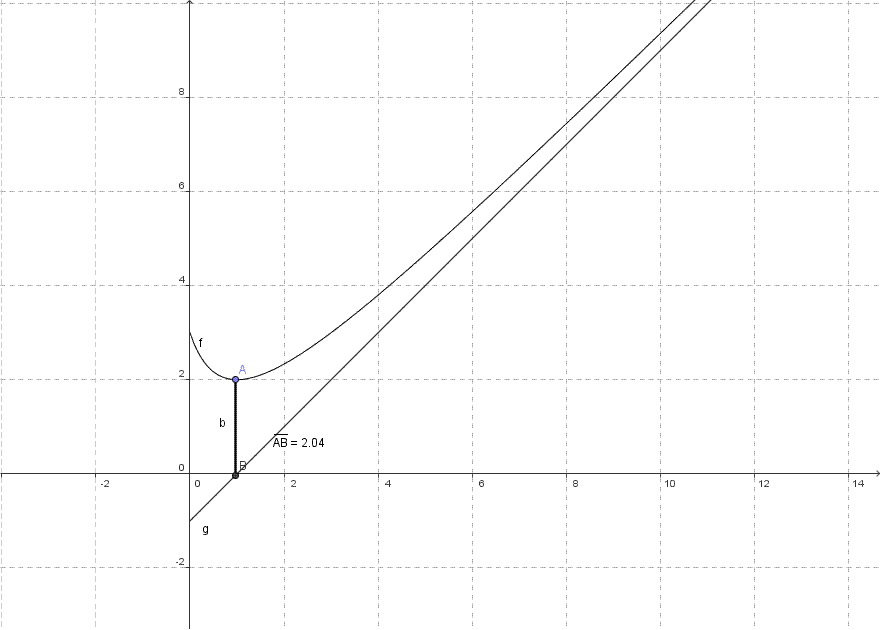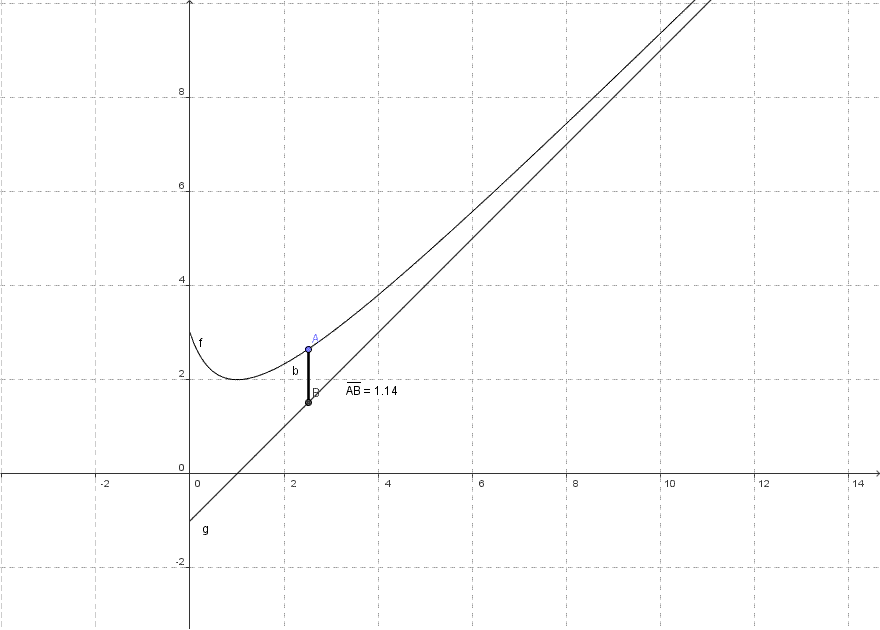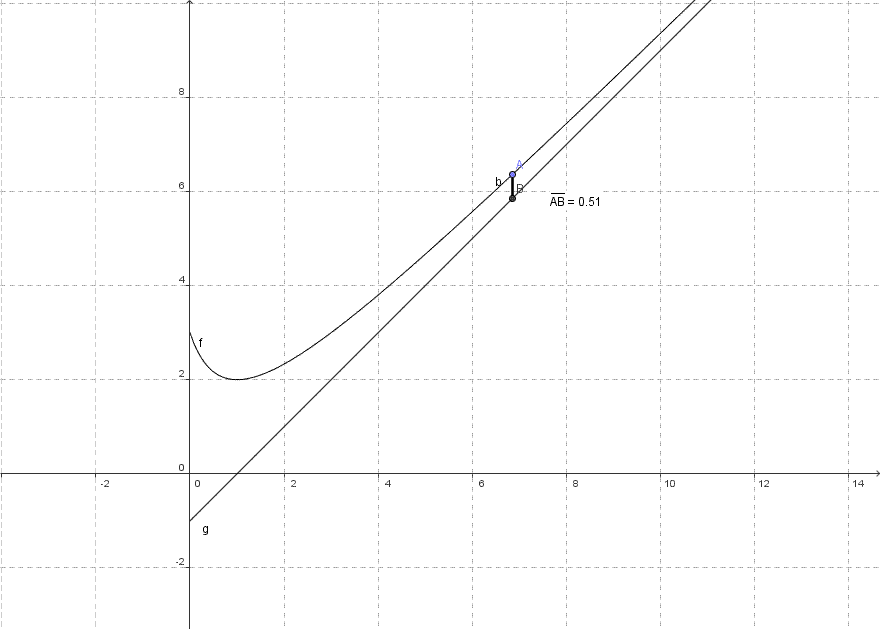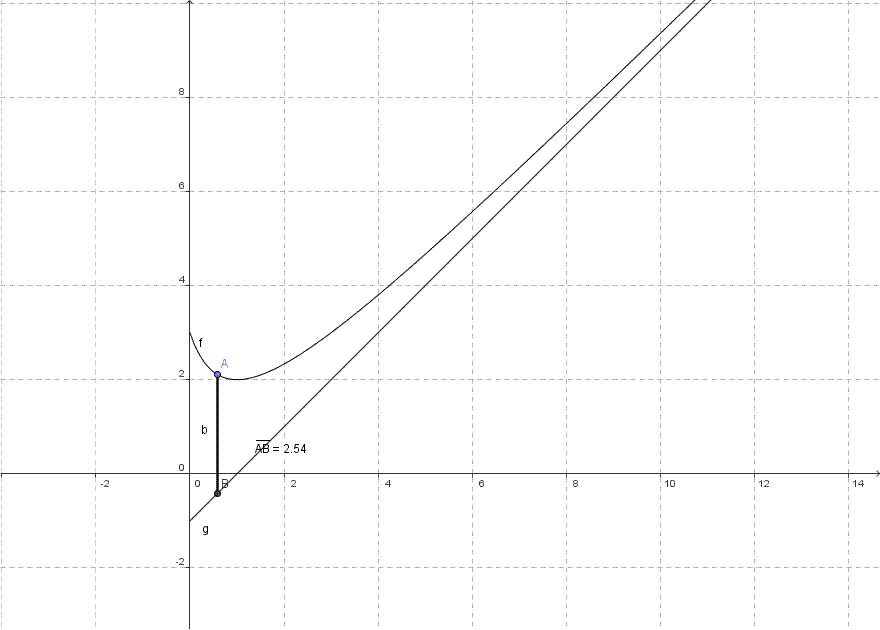
You might be thinking why they named these notations after Asymptotes, right?

Well, the answer is - We're not referring to any curves or lines in this case. Here, the word just wants to convey the idea that some value is tending to a particular value(or the limiting value) and as it gets closer and closer to that value( or we can say tending to the limiting value), the algorithm would stop executing as it reaches its termination point. Then we can express the complexity of the algorithm based on that limiting value.

Types of Asymptotic Notations

We've already discussed about the types of scenarios that we might encounter while making an algorithm. Summing it all up, there can be best case, average case and worst case scenarios.

Best Case Scenario is the condition of wherein the algorithm would take the least time possible. Whereas, Worst Case Scenario is for the condition wherein the algorithm takes the most time.

All the cases that come in between worst and best case are called Average Case Scenarios.

Now, there are separate types of notations to describe each of the above three scenarios. They're as follows:

1. Big O Notation - Represented by O. It is used to describe the worst case scenario of an algorithm.
2. Omega Notation - Represented by Ω. It is used to describe the best case scenario of an algorithm.
3. Theta Notation - Represented by θ. It is used to describe all the cases falling between then worst and best case or we can say the average case scenarios of an algorithm.

There's a much deeper and mathematical definition of these notations. But, we're not gonna touch that part of this topic in this post.

In order to represent these notations, you write the symbol of these notations first and then within the bracket adjacent to the symbol you write the function that best defines the complexity of algorithm. Like this -

O(n) - for Big O notation

Ω(n) - for omega notation

θ(n) - for theta notation

Here n denotes a function, you can write any other function inside the brackets.

An Example

Now, lets understand the whole concept with an example.

Suppose you're given the task of making a program to get an array of numbers from the user. Just like any other normal person, you think of doing it by using the for-loop.

But wait! There's a problem. A for-loop needs a parameter or a limit up to which the loop would function. In this case that would be the number of items that the user will be entering into the array(or the array size). Let's divide this problem in scenarios.

Scenario No. 1

You already know the number of elements. Let's say it is 5.

Then you simply have to set the limit as 5 in the for loop, like this -

for(int i=0; i<5; i++){
    printf("Enter number: ");
    scanf(" %d", &array[i]);
}

Now, the complexity of the algorithm for this code would be O(1).

O(1) means that the algorithm would take constant time for its execution as we can see that there are no unknown variables in it.

Scenario No. 2

You don't know the number of elements.

What can you possibly do in that case? Probably ask for the number of elements the user wants to enter directly in the program and then set the limit in the for-loop, right?

That would be something like this -

for(int i=0; i<n; i++){
    printf("Enter number: ");
    scanf(" %d", &array[i]);
}

Now, you don't really know the value of "n".

This is definitely not gonna execute in constant time as now its execution depends on the value of "n". We can represent it as - O(n). So in this case, the performance of the algorithm will grow linearly with the value of "n".

You can also take other code examples and check their Big O notations. Like - suppose you want to find the complexity of algorithm when you want to get the elements of a matrix from the user. Suppose it is n*n matrix. The code this would be something like this -

for(int i=0; i<n; i++){
    for(int j=0; j<n; j++){
        printf("Enter number: ");
        scanf(" %d", &array[j]);
    }
}

This means, its gonna accept the input for every i'th row and j'th column up to when both and i and j reach the value of n. So, Big O of algorithm for this code would be -

O(n*n) or O(n²)

Note that all these problems have been discussed only on the basis of their worst case scenarios(that's why we've used Big O Notation).

Based on problems, you might come across many types of asymptotic notations. You might not know which notation is better than which. Here's a graph to clarify that for you -

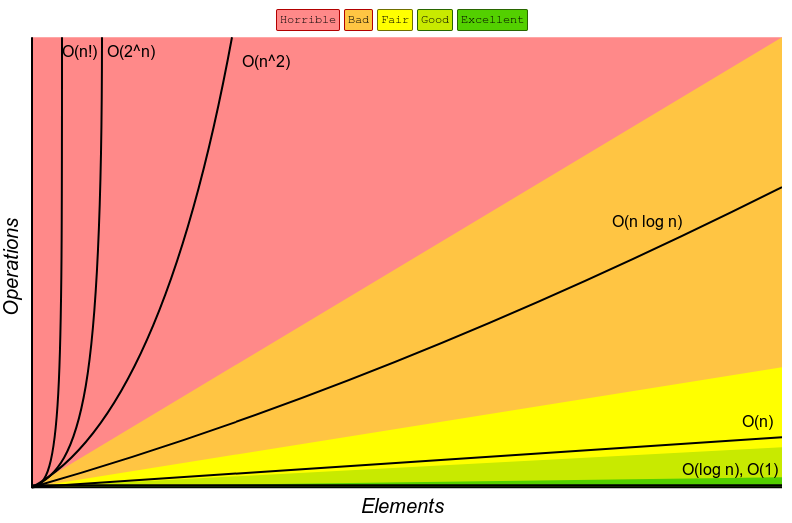
Fin.

There are many more concepts attached to this topic but I chose to present it in as simple way as I could as it was just to give you basic introduction of this topic. We'll build upon it more and more as we come across different kinds of data structures in the future.

I hope you liked reading this article. For more articles like this one, you can check the link right here.

Thanks for reading!✨